Chapters
In this article, we have compiled formulas related to a circle. Before proceeding to the formulas, first, let us see what is a circle.
In mathematics and geometry, a circle is a two-dimensional figure which is described in terms of its radius. A circle segregates the plane into two regions: interior and exterior. It is a type of ellipse that has zero eccentricity. The two foci of the circle are coincident. We can also say that a circle is the locus of points drawn at an equal distance from the center. The radius of the circle refers to the distance between the circle and its outer line. A diameter divides the circle into two equal parts and is two times the radius of the circle. A circle also has its area and perimeter. Its perimeter is referred to as the circumference of the circle and it reflects the distance around the circle. Examples of circular-shaped objects in real life include wheels, rings, coins, buttons, dartboard, and hula hoops.

Circle Area
The area of the circle is the space occupied by the circle. The formula for the area of the circle is given in terms of its radius. The area of the circle is calculated using the following formula:
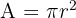
In the above formula, the Greek letter  depicts the constant ratio which is equal to 3.1416.
depicts the constant ratio which is equal to 3.1416.
Consider the following example.
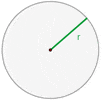
The radius of the following circle is 5 cm. Calculate the area of the circle

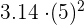
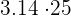
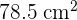
Circle Perimeter
In geometry, the perimeter of the circle or ellipse is known as the circumference of the circle. Generally, the perimeter depicts the length of the curve around any closed figure.
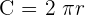
 represents a fixed value that is equal to 3.1416.
represents a fixed value that is equal to 3.1416.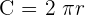
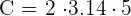
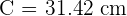
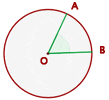
Arc Length
Arc is the most important element of the circle after radius and diameter. The arc of the circle reflects the portion of the circumference of a circle. We know that the circumference of the circle is the distance around the circle. Hence, we can say that the circumference of the circle is a full arc of the circle itself.
The formula for an arc length of the circle is given below:
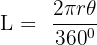
Here, r is the radius of the circle
 represents the angle subtended by the arc at the center of the circle
represents the angle subtended by the arc at the center of the circle
 has a fixed value of 3.1416
has a fixed value of 3.1416
In the figure below the length of the arc is the distance from point A to B.
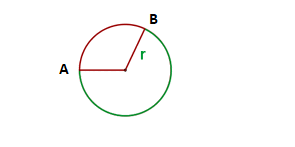
 =
= 
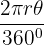
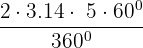

Circular Sector Area
A circular sector is the part of the circle that is enclosed by two radii and an arc. The formula for the area of the circular sector is given below:

In the figure below, the area of the sector of the circle is the area covered by the sector (shown in red) of the circle.
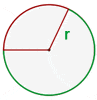
Suppose the angle created by two radii of the above circle is equal to 70 degrees and the radius is equal to 7 cm. What is the area of the sector?
Radius of the circle = r = 7 cm
Angle created between two radii of the circle = 70 degrees
Area of the sector = A = 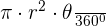
= 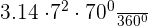
= 
Area of a Circular Segment
This part of the circle is enclosed between a chord and the corresponding arc of the circle. The grey circular segment of the circle is shown in the figure below:

The formula for area of the segment of the circle is given below:
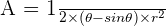
Lune of Hippocrates
In geometry, the lune of Hippocrates which is named after Hippocrates of Chios refers to the lune bounded by two arcs of the circle.
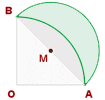
Area of the lune = area of the semicircle − area of the circular segment.
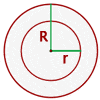
Area Enclosed between Two Concentric Circles
The circles having a common center are referred to as concentric circles. The area between two concentric circles of varying radii is known as an annulus. Two concentric circles of radii R and r are shown in the figure below:

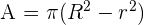
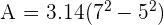
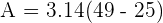
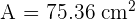
Area of a Circular Trapezoid
Calculating the area of the circular trapezoid is quite difficult. To comprehend the area of the circular trapezoid, you should know the circular sectors because the area of the circular trapezoid is equal to the difference between the area of the largest and smaller circular sector. The formula for calculating the area of the sector is:
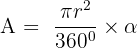
We already know that the area enclosed between two concentric circles is equal to:
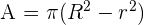
Hence, the area of the sector is:
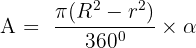
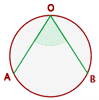
Angles in a Circle
In this section, we have compiled a list of formulas related to the angles of the circle.
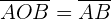
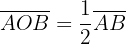

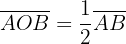

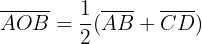

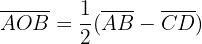
Summarise with AI:












Hi Emma nice to meet u I love reading and solving mathematics problem