Chapters

What is a Line
| Definition | |
| Line | A one-dimensional element that is straight |
A line is the very basic unit of any shape. It is one dimensional because it only has one dimension: length. When you draw a line, it is drawn with two arrows at each end.

What is a Line Segment
Line segments are usually what people think about when they imagine lines. Let’s take a look at the definition of a line segment.
| Definition | |
| Line Segment | A one-dimensional element that is a straight line between two points and doesn’t go beyond these two points |
You can also think of a line segment as a specific part of a line. Take a look below.

| Notation | |
| Line Segment | overline{AB} |
The notation for a line segment is simply the two points or name of the line with a straight line over it. Lines are usually written as one or two capital letters:
| Notation | Example | |
| Name of the line | 1 capital letter | L |
| Two points of the line | 2 capital letters | overline{AB} |
Parallel Lines
When we talk about lines, we usually are referring to either line segments or two other types of lines. These lines are parallel and perpendicular lines. In order to understand what perpendicular lines are, let’s see what parallel lines are first.
| Definition | |
| Parallel lines | Lines that are always the same distance from each other and never cross, or intersect |
These are the properties that all parallel lines have, regardless of whether they are lines or line segments. Let’s take a look at the notation for parallel lines.
| Notation | |
| Parallel lines | overline{line ; 1} ; perp ; overline{line ; 2} |
Here is an example of two parallel line segments and lines.

| Notation | |
| A | overline{AB} ; perp ; overline{CD} |
| B | overline{L} ; perp ; overline{M} |
What are Perpendicular Lines
Now that you understand the basics of lines, we can now define perpendicular lines. To be perpendicular means that two lines intersect, or cross, at a 90 degree angle.
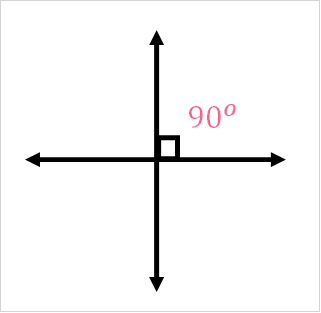
| On lines | Written |
| Squares at the angles | 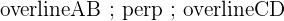 |
Slope Test for Perpendicular Lines
Now that you have seen what perpendicular lines are, you may be wondering - is there a way to test whether or not two lines are perpendicular? The easiest way is to check to see if the angle is 90 degrees.
If you don’t know the angle, you can use the slope test. When two lines are perpendicular, they have reciprocal slopes. See the example below.
[
frac{3} = frac{1}{3}
]
What Does Congruent Mean?
Another important concept related to perpendicular lines is called congruency. This can refer to lines, shapes and even three dimensional objects. Let’s focus on lines and line segments.
When two lines are congruent, it means that they have the same length. Take a look at the notation below.
[
overline{AB} ; cong ; overline{CD}
]
Another way to tell whether two lines are congruent is when they have dash marks on them of the same number.
What is Perpendicular Bisector
A perpendicular bisector is another way in which two lines can interact with each other. Perpendicular bisectors refer to two perpendicular lines.
What’s special about perpendicular bisectors is that the lines bisect each other. Bisect, in maths, means that the line or shape is divided exactly in half.
This means that each bisected line is congruent to each other when two lines are perpendicular bisectors.
Perpendicular Bisector Theorem
The perpendicular bisector theorem is a continuation of the idea of perpendicular bisectors. Imagine two perpendicular lines 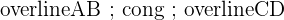 .
.
Say you draw a point on 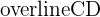 above the intersection point. If you were to connect that point to the end of the line
above the intersection point. If you were to connect that point to the end of the line  on either side, both of these lines would have the same length.
on either side, both of these lines would have the same length.
In other words, this drawn point would be equidistant to the endpoints of  .
.
Circumcentre of a Triangle
Imagine you have a triangle. Take one side of that triangle and draw a line that is perpendicular to it. If you repeat this three times, you have each side of the triangle and the lines that are perpendicular to each of those sides.
These lines all intersect at one point inside of the triangle. This point of intersection is called the circumcentre of the triangle.
Circumcircle
Now that you know what the circumcentre of a triangle is, imagine that the circumcentre is now the centrepoint of a circle. This circle, at the same time, touches each of the three points of the triangle.
This circle is called a circumcircle.












Hi Emma nice to meet u I love reading and solving mathematics problem