Chapters

Introduction
In the real world, geometry problems don't always come with a neatly drawn shape and a big "Calculate Area" sign. Instead, they come as stories or scenarios: a gardener needing to know how much turf to buy, a painter calculating the paint for a wall, or a builder planning a pathway.
Solving area word problems requires a two-step process:
- Translate the English into Math: Read the problem carefully to identify the shapes involved and their dimensions. Draw a quick sketch if it helps!
- Apply the Correct Formulas: Once you know the shapes, use the standard area formulas to perform the calculations.
Square: Area = side 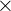
Rectangle: Area = length 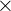
Triangle: Area = ½ 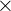
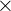
Trapezoid: Area = ½ 
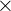
Practice Questions & Answers
A square garden with a side length of 150 m has a square swimming pool in the very centre with a side length of 25 m. Calculate the area of the garden (excluding the pool).
To find the area of the garden, we must subtract the area of the pool from the total area of the square plot.
Calculate the total area of the square plot: Area (total) = 150 m x 150 m = 22,500 m²
Calculate the area of the square pool: Area (pool) = 25 m x 25 m = 625 m²
Subtract the pool's area from the total area: Area (garden) = 22,500 m² - 625 m² = 21,875 m²
Answer: 21,875 m²
A rectangular garden has dimensions of 30 m by 20 m and is divided into 4 parts by two pathways that run perpendicular from its sides. One pathway has a width of 0.8 m and the other, 0.7 m. Calculate the total usable area of the garden.

To find the usable area, we calculate the total area of the large rectangle and subtract the area of the two pathways.
Total area of the garden: 30 m x 20 m = 600 m²
Area of the pathway parallel to the 30 m side (width 0.7 m): 30 m x 0.7 m = 21 m²
Area of the pathway parallel to the 20 m side (width 0.8 m): 20 m x 0.8 m = 16 m²
Note that the two pathways overlap in the center. The overlapping rectangle has dimensions 0.8 m by 0.7 m. We must subtract this overlap once so we don't count it twice. Overlap Area = 0.8 m x 0.7 m = 0.56 m²
Total area of pathways = Area1 + Area2 - Overlap Total Path Area = 21 + 16 - 0.56 = 36.44 m²
Usable Area = Total Garden Area - Total Path Area Usable = 600 - 36.44 = 563.56 m²
Answer: 563.56 m²
Calculate the area of the quadrilateral that results from drawing lines between the midpoints of the sides of a rectangle whose base and height are 8 cm and 6 cm respectively.
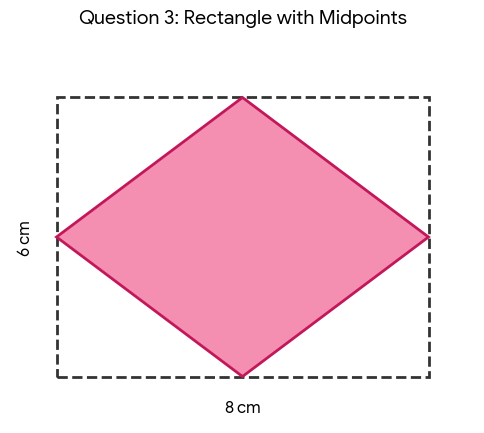
When you connect the midpoints of any rectangle, the resulting shape is a rhombus.
There is a useful property for this scenario: the area of the inner quadrilateral (the rhombus) is exactly half the area of the original rectangle.
Calculate the area of the outer rectangle: Area (rect) = base x height = 8 cm x 6 cm = 48 cm²
The area of the inscribed quadrilateral is half of this: Area (quad) = ½ x 48 cm² = 24 cm²
Answer: 24 cm²
A line connects the midpoint of BC (Point E), with Point D in the square ABCD shown below. Calculate the area of the acquired trapezoid shape (ABED) if the square has a side of 4 m.
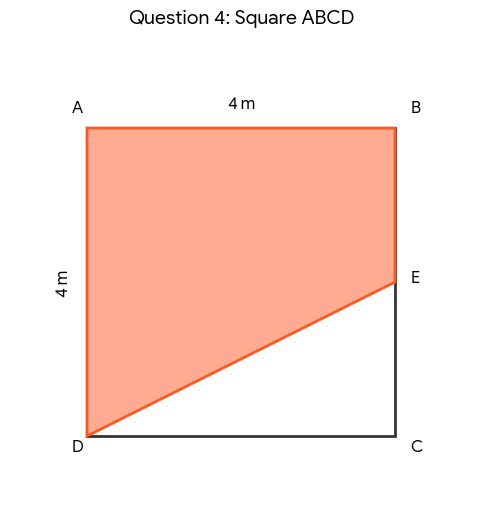
We need to find the area of the trapezoid ABED. The formula for a trapezoid is: Area = ½ x (base1 + base2) x height.
Looking at the shape ABED:
The parallel sides are DA and EB.
Length of DA = side of the square = 4 m.
Length of EB = Since E is the midpoint of BC, EB is half the side length = 4 / 2 = 2 m.
The height of the trapezoid is the perpendicular distance between the parallel sides, which is the side AB.
Height (AB) = 4 m.
Now, substitute these values into the formula: Area = ½ x (DA + EB) x AB
Area = ½ x (4 + 2) x 4 = 12 m²
Answer: 12 m²
Calculate the amount of paint needed to paint the front of this building knowing that 0.5 kg of paint is needed per m².
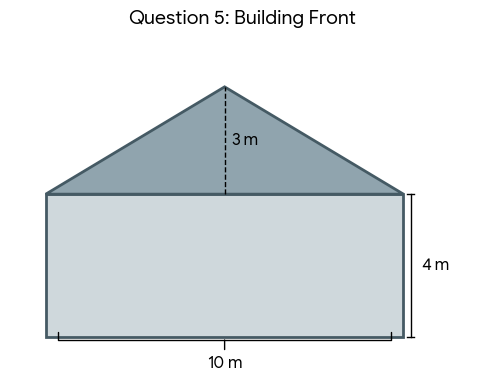
First, we must calculate the total area of the building's front. We can divide the shape into a rectangle and a triangle.
Area of the rectangle:
Base = 10 m
Height = 4 m
Area (rect) = 10 x 4 = 40 m²
Area of the triangle (the roof):
Base = 10 m (same as the rectangle)
Height of the triangle = Total height - Height of rectangle = 7 m - 4 m = 3 m.
Area (tri) = ½ x base x height = ½ x 10 x 3 = 15 m²
Total Area:
Total Area = 40 m² + 15 m² = 55 m²
Calculate paint needed:
We need 0.5 kg of paint for every 1 m².
Total paint = Total Area x 0.5 kg/m²
Total paint = 55 x 0.5 = 27.5 kg
Answer: 27.5 kg
A wooded area is in the shape of a trapezoid whose bases measure 128 m and 92 m and its height is 40 m. A 4 m wide walkway is constructed which runs perpendicular to the two bases. Calculate the area of the wooded area after the addition of the walkway.
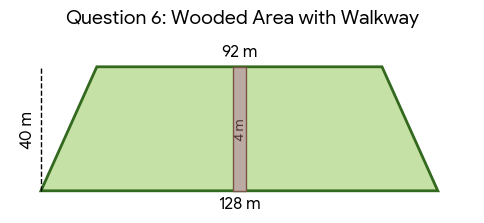
To find the final area, we calculate the original area of the trapezoid and subtract the area of the rectangular walkway.
Calculate the original area of the trapezoid:
Formula: Area = ½ x (base1 + base2) x height
Area (trap) = ½ x (128 + 92) x 40 = 4,400 m²
Calculate the area of the walkway:
The walkway is a rectangle that runs between the two bases, so its length is equal to the height of the trapezoid (40 m), and its width is given as 4 m.
Area (walkway) = length x width = 40 x 4 = 160 m²
Calculate the final wooded area:
Final Area = Original Area - Walkway Area
Final Area = 4,400 - 160 = 4,240 m²
Answer: 4,240 m²
A farmer has a rectangular field that is 200 m long and 150 m wide. He wants to apply fertilizer to the field. One bag of fertilizer covers an area of 500 m². How many bags of fertilizer must he buy to cover the entire field?
Calculate the total area of the field: Area = length x width = 200 m x 150 m = 30,000 m²
Determine how many bags are needed: Number of bags = Total Area / Area per bag
Number of bags = 30,000 / 500 = 60 bags
Answer: 60 bags
The sail of a boat is in the shape of a right-angled triangle. The base of the sail is 6 m long and the height is 12 m. If the material for the sail costs £15 per square meter, what is the total cost of the material for the sail?
Calculate the area of the triangular sail: Area = ½ x base x height Area = ½ x 6 x 12 = 36 m²
Calculate the total cost: Cost = Area x Cost per m²
Cost = 36 x £15 = £540
Answer: £540
A tiler is tiling a square floor. The floor has a side length of 8 m. The tiles are square with a side length of 50 cm. How many tiles will be needed to cover the floor?
First, ensure all units are the same. Let's work in meters.
Tile side length = 50 cm = 0.5 m
Calculate the area of the square floor: Area (floor) = 8 m x 8 m = 64 m²
Calculate the area of one tile: Area (tile) = 0.5 m x 0.5 m = 0.25 m²
Divide the floor area by the tile area to find the number of tiles: Number of tiles = 64 / 0.25 = 256 tiles
Answer: 256 tiles
A city is building a new park in the shape of a trapezoid. The two parallel sides of the park measure 1.2 km and 0.8 km. The perpendicular distance between them is 0.5 km. What is the area of the new park in square kilometers (km²)?
We use the area formula for a trapezoid: Area = ½ x (base1 + base2) x height
Area = ½ x (1.2 + 0.8) x 0.5 = 0.5 km²
Answer: 0.5 km²












Hi Emma nice to meet u I love reading and solving mathematics problem