In this article, we will discuss what are coplanar vectors with examples.
The vectors that lie on the same plane in a three-dimensional space are referred to as coplanar vectors. These vectors are parallel to the same plane. We can easily find any two random coplanar vectors in a plane. If two lines are coplanar in a three-dimensional space, then we can represent them in a vector form. The scalar triple product of the coplanar vectors is always equal to zero.

Conditions for Coplanar vectors
- If the scalar triple product of three vectors in 3D space is equal to zero, then we can say that these three vectors are coplanar.
- If three vectors in a 3D space are linearly independent, then the vectors are coplanar.
- If we have 'n' vectors and a maximum of two vectors linearly independent, then we can say that all the 'n' vectors are coplanar.
To determine whether the three vectors are coplanar or not, we often find the scalar triple product of the three vectors. The scalar triple product, also known as a mixed product, is the scalar product of three vectors. The scalar triple product of three vectors  ,
,  , and
, and  can be mathematically denoted like this:
can be mathematically denoted like this:

This product is equal to the dot product of the first vector  by the cross product of other two vectors
by the cross product of other two vectors 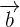 and
and  . It is referred to as a scalar product because just like a dot product, the scalar triple product gives a single number. Mathematically, the scalar triple product is represented as:
. It is referred to as a scalar product because just like a dot product, the scalar triple product gives a single number. Mathematically, the scalar triple product is represented as:
 =
= 
In the next section, we will solve a couple of examples in which we will determine whether the given vectors are coplanar or not by using the scalar triple product.
Example 1
Determine if point A = (5, 2, 3), B = (1, 6, 7) and C = (4, 2, 5) are coplanar or not.
Solution
The points A, B, and C will be coplanar if the scalar triple product of  ,
,  , and
, and  is equal to zero.
is equal to zero.
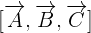 =
= 
First, we will find the cross product of  by using a determinant. The elements of the determinant will be the coordinates of these vectors.
by using a determinant. The elements of the determinant will be the coordinates of these vectors.
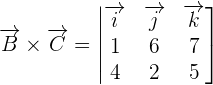
We will use the formula for finding a determinant of 3 x 3 matrix to calculate the cross product of 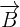 and
and 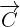 .
.
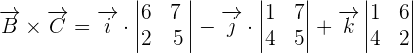
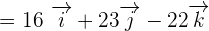
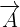 and
and 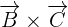 like this:
like this: 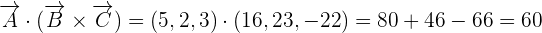
Hence, we can conclude that the point A, B, and C are not coplanar because the scalar triple product of the three vectors is not zero.
Example 2
Determine if points A = (0, 1, -1), B = (4, 3, 1) and C = (3, 2, 1) are coplanar or not.
Solution
The points A, B, and C will be coplanar if the scalar triple product of  ,
,  , and
, and  is equal to zero.
is equal to zero.
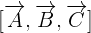 =
= 
First, we will find the cross product of  by using a determinant. The elements of the determinant will be the coordinates of these vectors.
by using a determinant. The elements of the determinant will be the coordinates of these vectors.

We will use the formula for finding a determinant of 3 x 3 matrix to calculate the cross product of 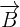 and
and 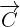 .
.
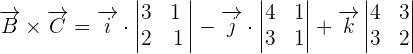

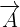 and
and 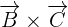 like this:
like this: 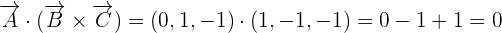
Hence, we can conclude that the point A, B, and C are coplanar because the scalar triple product of the three vectors is equal to zero.
Example 3
Determine if points A = (5, 1, 1), B = (3, 3, 1) and C = (2, 2, 1) are coplanar or not.
Solution
The points A, B, and C will be coplanar if the scalar triple product of  ,
,  , and
, and  is equal to zero.
is equal to zero.
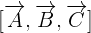 =
= 
First, we will find the cross product of  by using a determinant. The elements of the determinant will be the coordinates of these vectors.
by using a determinant. The elements of the determinant will be the coordinates of these vectors.
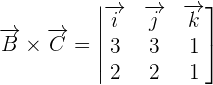
We will use the formula for finding a determinant of 3 x 3 matrix to calculate the cross product of 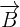 and
and 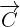 .
.
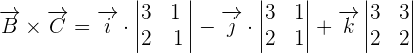
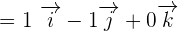
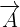 and
and 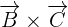 like this:
like this: 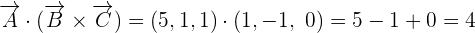
Hence, we can conclude that the point A, B, and C are not coplanar because the scalar triple product of the three vectors is not equal to zero.
So far, we have solved the problems in which we were given three points. Now, we will start solving the questions in which four points will be given and we will check the coplanarity of those 4 points. So, let us get started.
Example 4
Are four points A = (2, 3, 5), B = (4, 1, 6), C = (1,8, 4), and D = (1, 6, 4) coplanar?
Solution
To find whether these points are coplanar or not, first, we will find 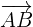 ,
, 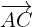 and
and 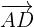 like this:
like this:
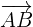 = (4 - 2, 1 - 3, 6 - 5) = (2, -2, 1)
= (4 - 2, 1 - 3, 6 - 5) = (2, -2, 1)
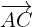 = (1 - 2, 8 - 3, 4 - 5) = (-1, 5, -1)
= (1 - 2, 8 - 3, 4 - 5) = (-1, 5, -1)
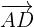 = (1 - 2, 6 - 3, 4 - 5) = (-1, 3, -1)
= (1 - 2, 6 - 3, 4 - 5) = (-1, 3, -1)
Now, we will find the determinant of the above vectors like this:

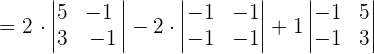

Since, the scalar triple product is not equal to zero, hence the points A, B, C, and D are not coplanar.
Example 5
Are four points A = (1, 5, 7), B = (6, 3, 1), C = (2 ,9, 5), and D = (7, 6, 5) coplanar?
Solution
To find whether these points are coplanar or not, first, we will find 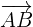 ,
, 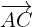 and
and 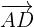 like this:
like this:
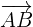 = (6 - 1, 3 - 5, 1 - 7) = (5, -2, -6)
= (6 - 1, 3 - 5, 1 - 7) = (5, -2, -6)
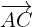 = (2 - 1, 9 - 5, 5 - 7) = (-1, 4, -2)
= (2 - 1, 9 - 5, 5 - 7) = (-1, 4, -2)
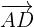 = (7 - 2, 6 - 5, 5 - 7) = (6, 1, -2)
= (7 - 2, 6 - 5, 5 - 7) = (6, 1, -2)
Now, we will find the determinant of the above vectors like this:

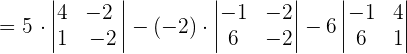
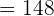
Since, the scalar triple product is not equal to zero, hence the points A, B, C, and D are not coplanar.













Hi Emma nice to meet u I love reading and solving mathematics problem