Chapters
- Intersection of Planes
- 1. Intersecting at a Point
- 2.1 Each Plane Cuts the Other Two in a Line.
- 2.2 Two Parallel Planes and the Other Cuts Each in a Line
- 3.1 Three Planes Intersecting in a Line
- 3.2 Two Coincident Planes and the Other Intersecting Them in a Line
- 4.1 Three Parallel Planes
- 4.2 Two Coincident Planes and the Other Parallel
- 5. Three Coincident Planes
- Examples
The current research tells us that there are 4 dimensions. These four dimensions are, x-plane, y-plane, z-plane, and time. Since we are working on a coordinate system in maths, we will be neglecting the time dimension for now. These planes can intersect at any time at any place. There is no definite saying that whether they all will intersect or some of them will or maybe none of them might intersect each other. The question is how to identify whether planes are intersecting with each other? Let's figure it out!

Intersection of Planes
The best and possible way to learn about their intersection is using the rank method. Below is a small matrix of three planes.
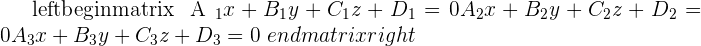
To study the intersection of three planes, form a system with the equations of the planes and calculate the ranks.
r = rank of the coefficient matrix.
r'= rank of the augmented matrix.
There is a lot of possibilities for plane intersections. That is why we listed all kinds of possibilities and their identifications. The relationship between the three planes presents can be described as follows:
1. Intersecting at a Point
When all three planes intersect at a single point, their rank of the coefficient matrix, as well as the augmented matrix, will be equal to three.
r=3, r'=3

2.1 Each Plane Cuts the Other Two in a Line.
So you have learned about a single point, what if it was a line? And there might be a chance of two lines intersection too. This type of intersection will create a prismatic surface. The rank of the coefficient matrix will be two, however, the rank of the augmented matrix will be equal to three.
r = 2, r' = 3

2.2 Two Parallel Planes and the Other Cuts Each in a Line
Same line scenario but a single plane cuts both parallels planes making a line intersection. The rank of the coefficient matrix will be two while the rank of the augmented matrix will be three.
r = 2, r' = 3
Two rows of the coefficient matrix are proportional. This is an identification of two parallel planes and the other cuts each in a line.
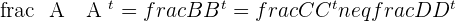

3.1 Three Planes Intersecting in a Line
There is a possibility that all three planes will intersect each other but not at a certain point but on the line. This can happen and the best way for its identification is that if the rank of the coefficient matrix, as well as the augmented matrix, is equal to two.
r = 2, r' = 2

3.2 Two Coincident Planes and the Other Intersecting Them in a Line
If two planes are coincident and the third plane is intersecting in a way that it creates a line then their rank of the coefficient matrix, as well as the augmented matrix, will also be equal to two but with a twist. The two rows of the augmented matrix will be proportional.

r = 2, r' = 2
4.1 Three Parallel Planes
What if none of those planes intersects at any point but they are parallel? Then their rank of the coefficient matrix will be one, however, the rank of the augmented matrix will be two.
r = 1, r' = 2

4.2 Two Coincident Planes and the Other Parallel
If two planes are coincided and the third one is parallel then the rank will be the same, the rank of the coefficient matrix will be one while the rank of the augmented matrix will be two. However, the point to notice is that the two rows of the augmented matrix will be proportional, which is the indication that you are working with two coincident planes while the other plane is parallel.

r = 1, r' = 2

5. Three Coincident Planes
Last but not least, are all three planes coincident? Not an issue! Both ranks, rank of the coefficient matrix as well as rank of the augmented matrix, will be equal to one.
r = 1, r' = 1

Examples
State the relationship between the three planes.
1. 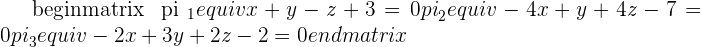
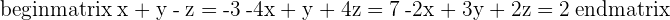


Each plane cuts the other two in a line and they form a prismatic surface.
2. 
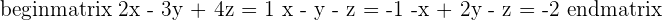
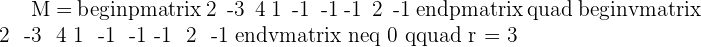
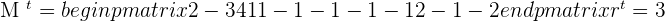
Each plan intersects at a point.
3. 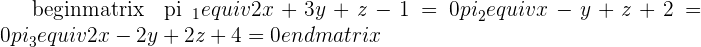
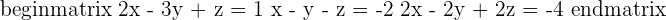
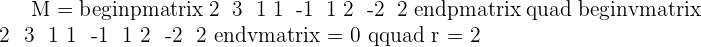
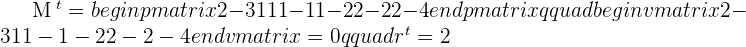
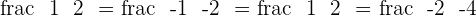
The second and third planes are coincident and the first is cuting them, therefore the three planes intersect in a line.
4. 
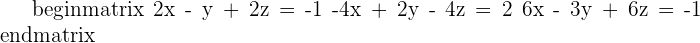

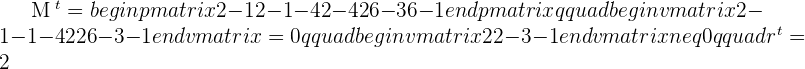

The first and second are coincident and the third is parallel to them.













Hi Emma nice to meet u I love reading and solving mathematics problem