Chapters
The Lune of Hippocrates in geometry is named after Hippocrates of Chios. It refers to the lune bounded by arcs of two circles. The diameter of the smaller of the two arcs is a chord that spans a right angle on the larger circle. In other words, we can say that the Lune of Hippocrates is a non-convex plane region bounded by two circular arcs: 180 degrees and 90 degrees. Lune of Hippocrates is considered as the first curved figure whose exact area was computed mathematically.

History of Lune of Hippocrates
Hippocrates of Chios wanted to solve a classic problem related to squaring the circle. This problem involved constructing a square having an area equal to the given circle using a compass and a straightedge. He proved that the area of the lune bounded by the arcs which are labeled E and F in the figure below is equal to the area of the triangle ABO.
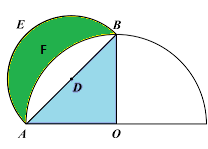
This created a hope of solving the classic problem about circle squaring because the lune is bounded by the arcs of circles only. According to Heath, Hippocrates was the first person who had proved that the area of the circle is proportional to the square of its diameter. He determined this important fact while proving his result. A book "History of Geometry" which was compiled by "Eudemus of Rhodes" contributed towards preserving the Hippocrates proof.
In the next section, we will discuss how to draw the Lune of Hippocrates.
Drawing the Lune of Hippocrates
Follow these steps to draw Lune of Hippocrates:
Step 1 - Draw a right-angled isosceles triangle AOB.
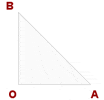
Step 2 - With center O, plot an arc between points AB.

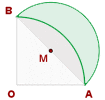
The outside, in green, is the lune of Hippocrates.
Area of the Lune
Area of the lune = area of the semicircle − area of a circular segment.
Area of the lune = area of the semicircle − (area sector − area of a triangle)
Area of the lune = 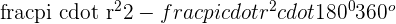 + area of the triangle
+ area of the triangle
Area of the lune = Area of the right triangle
In the next two examples, we will not only calculate the area of the lune but also prove that the area of the lune and the area of the right-angled triangle are equal.
Example 1
In the figure below, two semicircles are drawn. One of the semicircles is drawn on the side PQ of the triangle and the other is drawn on the side PR with the center O. What is the area of the grey shaded region which is bounded by two semicircles?
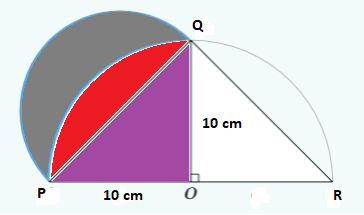
Solution
We already know that the grey shaded region is referred to as a lune.
We are unaware of the method to calculate the area of the grey shaded region, i.e., a lune. However, we know that it is somehow related to the area of other regions which we can calculate easily using the given parameters in the figure.
We have a right-angled triangle POQ. The formula for calculating the area of the right-angled triangle is:
Area = 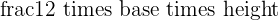
In this example, the base of the triangle POQ is 10 cm and its height is also 10 cm. Now, we know the height and base of the triangle, we can easily substitute it in the formula for calculating the area of the triangle as shown below:
Area = 
Area = 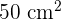
We know that the areas of the right-angled triangle and lune are equal. However, in the next section of this example, we are going to prove this fact.
We have colored the region of the figure in this example so that we can prove the Lune of Hippocrates rule and find the required area of the lune.
The purple and red regions of the above figure together make a quarter of the circle with radius 10 cm. So, the area of the quarter of the circle will be:
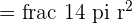

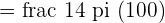
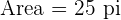
The grey and red regions regions together make a semi-circle whose diameter is equal to the hypotenuse of the triangle. The length of this hypotenuse is equal to  . Hence, the radius of the semi-circle is equal to
. Hence, the radius of the semi-circle is equal to 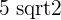 . Therefore, grey and red areas have a combined area of
. Therefore, grey and red areas have a combined area of 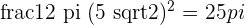 .
.
Combining these together, we can say that:
Grey + Red = Purple + Red (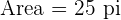 )
)
Hence, it is proved that the Grey and Purple regions have the same area. Thus, we can conclude that the grey lune has an area of 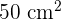 , the same as the Purple shaded right angle triangle.
, the same as the Purple shaded right angle triangle.
Example 2
In the figure below, two semicircles are drawn. One of the semicircle is drawn on the side AB of the triangle and the other is drawn on the side AC. What is the area of the green shaded region which is bounded by two semicircles?

Solution
Remember that the green shaded region is referred to as a lune.
We don't know how to calculate the area of the lune. However, we know that it is somehow associated with the area of other regions which we can calculate easily using the parameters in the figure.
We have a right angled triangle AOB. The formula for calculating the area of the right angled triangle is:
Area = 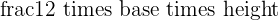
In this example, the base of the triangle AOB is 6 cm and its height is also 6 cm. Now, we know the height and base of the triangle, we can easily substitute it in the area of the triangle as shown below:
Area = 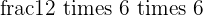
Area = 
We know area of right angle triangle is equal to the area of the lune. In the next section of this example, we will prove this fact.

We have now colored the regions of the original figure, so that we can specify them easily.
The blue and yellow regions of the above figure make a quarter of the circle with radius 6 cm. So, the area of the quarter of the circle will be:
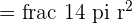

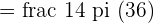
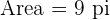
The green and yellow regions together make a semi-circle whose diameter is equal to the hypotenuse of the triangle. The length of this hypotenuse is equal to  . Hence, the radius of the semi-circle is equal to
. Hence, the radius of the semi-circle is equal to 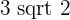 . Therefore, green and yellow areas have a combined area of
. Therefore, green and yellow areas have a combined area of  .
.
Combining these together, we can say that:
Blue + Yellow = Green + Yellow ( =  )
)
So, the blue and green areas are equal. Thus, we can conclude that the green lune has an area of  , the same as the blue triangle.
, the same as the blue triangle.













Hi Emma nice to meet u I love reading and solving mathematics problem