Chapters
Hexagon is one of the different types of polygon. In fact, a hexagon is usually known as one of the common representatives of the geometry polygon. For example, triangles and squares are also polygons but you would never say them a polygon because they have a specific name. The question is what is a regular hexagon then? Keep on reading to find your answer.

What is a Regular Hexagon?
A hexagon is a type of polygon that contains six sides. The word, "hex" is a Greek word that means "six". Usually, in polygons, the first word represents the sides of the polygon and the first word is usually a Greek word that represents a number. You might be thinking that regular hexagon is another name for hexagon, if you are thinking then, unfortunately, you are wrong. There are two types of hexagons, regular and irregular hexagons.
A regular hexagon is a polygon with six equal sides. If all six sides are equal that means all angles are also equal. The triangles formed by joining the centre with all the vertices, are equal in size and are equilateral. A regular hexagon is a convex geometrical shape. It means all the points of a regular hexagon will be pointing outside. On the other hand, an irregular hexagon will never have all six sides equal.
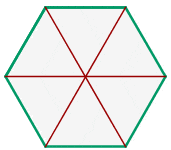
Angles of the Hexagon
The sum of all hexagon angles is equal to  . There are six sides of a hexagon, let's figure out other possible angles of a regular hexagon.
. There are six sides of a hexagon, let's figure out other possible angles of a regular hexagon.
The sum of interior angles of a hexagon = 
The value of an interior angle of the regular hexagon is 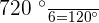
The central angle of the regular hexagon measures: 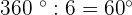
Diagonals of the Hexagon
A diagonal is a line that joins two non-adjacent vertices. A regular polygon has 9 diagonals.
The number of diagonals = 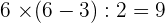

Apothem of a Regular Hexagon
Apothem is the distance of a line segment that is drawn from the centre of the polygon to the centre of any side of the regular hexagon. Let's calculate the apothem of a regular hexagon.
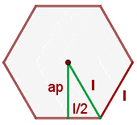
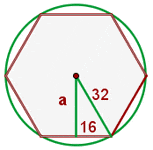
The first step is to draw the apothem as we did in the above diagram. If we draw another line segment from the centre of the regular hexagon to the vertex near to apothem, we could make a triangle. The best part of this triangle is that we can use the Pythagorean theorem to find the apothem of the regular hexagon. The line segment is equal to the side in length.
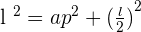

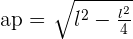


Perimeter of a Regular Hexagon
The perimeter of a regular hexagon shows the total length of the regular hexagon. To find the perimeter, you need to add all the sides of the regular hexagon. It means you need to add all six sides of the regular hexagon. Since a regular hexagon has all sides equal, we can conclude that:


Area of a Regular Hexagon
The area of a regular hexagon means the total space acquired by a regular hexagon. It is the half product of perimeter and apothem.

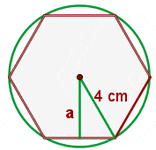
Calculate the apothem, perimeter and area of a regular hexagon inscribed in a circle with a radius of 4 cm.


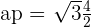

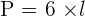
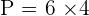
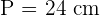


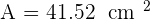
The area of a square is 2,304 cm². Calculate the area of a regular hexagon that has the same perimeter as this square.
Area of square = 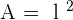

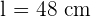
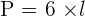
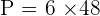
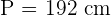

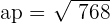

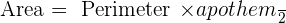
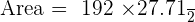
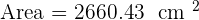













Hi Emma nice to meet u I love reading and solving mathematics problem