Ever saw a ball gear bearing? There are so many circles within circles. Finding geometric properties of circles isn't that hard now but, what if you are asked to find geometric properties in concentric circles? That is why we dedicated this resource to concentric circles and how to calculate their geometric properties.

What are Concentric Circles?
Take a pen and a piece of paper and draw a perfect circle. Within that circle, draw another circle and make sure the centre of both circles are the same. There you go, you have a concentric circle.

If you check textbooks, the definition you will find is that two circles are concentric if their centres coincide. The area enclosed between two concentric circles is also referred to as the annulus or circular ring. The biggest application of the concentric circle is the cylinder. A cylinder has a concentric circle. The thickness of the cylinder is the distance between the circumferences of both circles. However, the concentric circles we are talking about is in 2-Dimension, but if we expand it to 3-Dimension then it becomes a cylinder.
Area of the Annulus
To find the area of the annulus, you need to know the radius of both circles. Finding radius isn't that hard, all you need to know is the diameter of the circle and that divide it in half. Let's say that "r" represents the radius of the inner circle and "R" represents the radius of the outer circle. The area of a circle is:

We need to subtract the area of the inner circle from the area of the outer circle. The area of the inner circle is:

The area of the outer circle is:
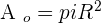
The area of the annulus equals the area of the larger circle minus the area of the smaller circle.
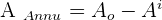
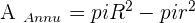
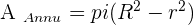
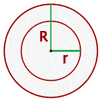
Circular Trapezoid

Now you know how to find the area of the annulus, however, you are interested in a small region of the annulus, not the whole annulus. To find the area of the specific region, we use another method. The area enclosed within the two radii and concentric circles is called the circular trapezoid.
Area of a Circular Trapezoid
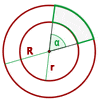
Finding the area of a circular trapezoid is tricky. To understand the area of the circular trapezoid, you need to know about the circular sectors. The area of the circular trapezoid is equal to the area of the largest circular sector minus the area of the smaller circular sector. The formula for the area of the sector is:

From area of annulus, we know that:
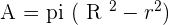
Let's replace it in the first equation:
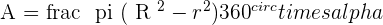
Examples
A circular fountain of 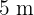 radius lies alone in the centre of a circular park of
radius lies alone in the centre of a circular park of  radius. Calculate the total walking area available to pedestrians visiting the park.
radius. Calculate the total walking area available to pedestrians visiting the park.

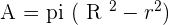
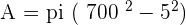
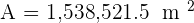
Calculate the area enclosed by the inscribed and circumscribed circles to a square with a diagonal of  in length.
in length.

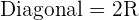
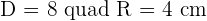
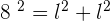


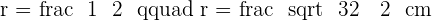
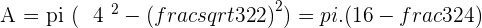
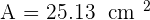
A regular hexagon of side  has a circle inscribed and another circumscribed around its shape. Find the area enclosed between these two concentric circles.
has a circle inscribed and another circumscribed around its shape. Find the area enclosed between these two concentric circles.
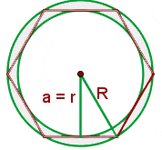

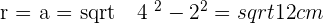

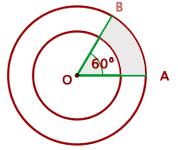
Two radii (plural for radius) OA and OB form an angle of 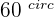 for two concentric circles with
for two concentric circles with  and
and 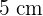 radii. Calculate the area of the circular trapezoid formed by the radii and concentric circles.
radii. Calculate the area of the circular trapezoid formed by the radii and concentric circles.














Hi Emma nice to meet u I love reading and solving mathematics problem