Chapters
In this article, you will learn what is a rectangle, its various parameters, and properties. You will also learn how to compute the area, perimeter, and length of the diagonal of the rectangle. So, let us get started.

What is a Rectangle?
A rectangle refers to a four-sided polygon in which all the internal angles are equal to 90 degrees. It has four vertices and two sides meeting at each vertex make a 90-degree angle. A rectangle has four sides and opposite sides of the rectangle have the same length. The primary difference between a square and a rectangle is that all four sides of the square are congruent, whereas in a rectangle only the opposite sides are congruent.
We can also say that a rectangle is a quadrilateral because it has four sides. In fact, we can say that a rectangle is an equiangular quadrilateral in which all the angles are equal. Length and width are important dimensions of the rectangle. The length and width of a rectangle should be of different sizes. If they are the same, then the given figure is a square, not a rectangle. The longer side is usually referred to as a length and the smaller side is known as the width of the rectangle. Consider the following rectangle ABCD.
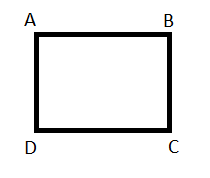
The above rectangle has four sides AB, BC, CD, and AD. The right angles are formed at the meeting points of the sides, i.e. vertices. The length of the rectangle is the distance between A and B or C and D. On the other hand, the width of the rectangle is distance between A and D, or B and C.
You can see that the opposite sides of the rectangle are always parallel to each other. In the above figure, side AB is parallel to DC, and side AD is parallel to BC.
Shape of Rectangle
A rectangle is a two-dimensional flat-shaped figure which is easier to represent in an XY- plane. Usually, the length of a rectangle in an XY plane is depicted by the arms of the x-axis and the width is shown by the arms of the y-axis. You may have seen several rectangular-shaped objects in your daily life. These objects include your mobile phone, TV screen, notebook, whiteboard, magazine, books, and tables, etc.
In the next section, we will discuss some of the properties of the rectangle.
Properties of Rectangle
A rectangle has the following properties:
- A rectangle has four sides and four vertices.
- At each vertex of the rectangle, a 90-degree angle is formed
- The opposite sides of the rectangle are parallel to each other and are congruent
- The diagonals of the rectangle bisect each other, i.e., they divide each other into two halves
- A rectangle can be considered as a parallelogram because of its parallel opposite sides.
- The sum of all the interior angles of a rectangle is equal to 360 degrees
- The diagonals of a rectangle are equal
- The area of the rectangle is equal to the product of its length and width
- The two diagonals of the rectangle divide it into two equal right angle triangles
- The diagonal of the rectangle can be calculated using the Pythagoras theorem
In the next section of the article, we will discuss how to calculate the area, perimeter, and diagonal of the rectangle.
Perimeter of a Rectangle
We can define the perimeter of the rectangle like this:
The total distance covered by the outer boundary of the rectangle is referred to as its perimeter
The formula for the perimeter of the rectangle is given below:
Perimeter = 2 (Length + Width)
Area of Rectangle
The area of the rectangle is defined as:
The region covered by the rectangle in a plane
The area is measured in square units as it is the product of its length and width.
The formula for the area rectangle is given below:
Area = Length x Width
Like other geometrical figures, the area of the rectangle is measured in square units.
Diagonal of a Rectangle
The length of the diagonal of a rectangle can be measured using the Pythagoras theorem because the diagonal divides the rectangle into two equal right-angle triangles. The diagonal "d" of the rectangle is shown below:

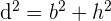
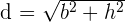
Example 1
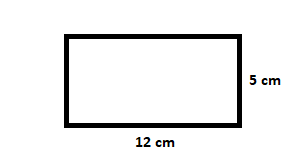
Calculate the area and perimeter of the following rectangle:
Solution
Length of the rectangle = L = 12 cm
Width of the rectangle = W = 5cm
Area = Length x Width
= 12 cm x 5 cm
= 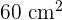
Perimeter of the rectangle = 2 (Length + Width)
= 2 (12 + 5)
= 2 (17)
= 34 cm
Example 2
Calculate the area and perimeter of the rectangle having length and width of 15 cm and 9 cm respectively. Calculate the length of the diagonal too.
Solution
Length of the rectangle = L = 15 cm
Width of the rectangle = W = 9 cm
Area = Length x Width
= 15 cm x 9 cm
= 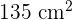
Perimeter of the rectangle = 2 (Length + Width)
= 2 (15 + 9)
= 2 (24)
= 48 cm
Length of the diagonal = 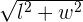
= 
= 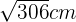
Example 3
Calculate the area and perimeter of the rectangle having length and width of 25 cm and 12 cm respectively. Also, calculate the length of the diagonal of the rectangle.
Solution
Length of the rectangle = L = 25 cm
Width of the rectangle = W = 12 cm
Area = Length x Width
= 25 cm x 12 cm
= 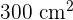
Perimeter of the rectangle = 2 (Length + Width)
= 2 (25 + 12)
= 2 (37)
= 74 cm
Length of the diagonal = 
= 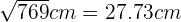
Example 4
The perimeter and width of the rectangle are 36 cm and 4 cm respectively. What is the area and length of the rectangle?
Solution
Perimeter of the rectangle = 36 cm
Width of the rectangle = 4 cm
Perimeter = 2 (Length + Width)
36 = 2 (L + 4)
36 = 2L + 8
36 - 8 = 2L
28 = 2L
L = 14 cm
Area of the rectangle = Length x Width
= 14 cm x 4 cm
= 56 
Example 5
The area and length of the rectangle are 45  and 9 cm respectively. What is the perimeter and width of the rectangle?
and 9 cm respectively. What is the perimeter and width of the rectangle?
Solution
Area of the rectangle = 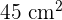
Length of the rectangle = 9 cm
Area of the rectangle = Length x Width
45 = Length x Width
45 = 9 x W
W = 5 cm
Perimeter of the rectangle = 2 (Length + Width)
= 2 (9 + 5) cm
= 2 (14) cm
= 28 cm
Example 6
The area and width of the rectangle are 191  and 11 cm respectively. What are the length, perimeter, and diagonal of the rectangle?
and 11 cm respectively. What are the length, perimeter, and diagonal of the rectangle?
Solution
Area of the rectangle = 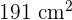
Width of the rectangle = 11 cm
Area of the rectangle = Length x Width
191 = Length x Width
191 = Length x 11
Length = 18 cm
Perimeter of the rectangle = 2 (Length + Width)
= 2 (18 + 11) cm
= 2 (29) cm
= 58 cm
Diagonal of the rectangle = 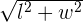
= 













Hi Emma nice to meet u I love reading and solving mathematics problem