In this article, we have compiled a list of geometry formulas which are quite helpful in solving the questions related to areas, volumes and perimeters of geometrical figures. So, let us get started.

Area and Perimeter Formulas
In this section, we have compiled a list of area and perimeter formulas of various geometrical figures.
Area of a geometrical figure refers to the amount of space in square length units occupied by the surface of the geometrical figure. On the other hand, a perimeter refers to the distance around the closed geometrical figure or shape.
Triangle
Triangle is one of the most fundamental shape in geometry that consists of three sides and three vertices. The sum of the interior angles of a triangle is equal to 180 degrees. The three types of triangle are equilateral, isosceles and scalene.
The formula for area of the triangle is:
Area = 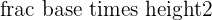
The formulas for perimeter of equilateral, isosceles and scalene triangles are a bit different. Basically, they all involve adding the length of three sides of the triangle.
Perimeter of an equilateral triangle = 3 x length of its side
Perimeter of an isosceles triangle = 2 x length + base

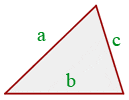
Perimeter of the scalene triangle = P = a + b + c
Square
Square refers to a regular quadrilateral which has four equal sides and angles. It means that all sides of the square are of the same length and all the angles are equal in measure.

Rectangle
A rectangle is a type of quadrilateral with four right angles. The opposite sides of the rectangle are of the same length and are parallel to each other.
Rhombus
A rhombus refers to a parallelogram with four equal sides and opposite equal angles. It means that all the four sides of the rhombus are of the same length and opposite angles are congruent.

 , here D and d represent the diagonals of the rhombus
, here D and d represent the diagonals of the rhombus
Rhomboid
A rhomboid is a type of parallelogram in which the adjacent sides have different lengths and angles are not equal to 90 degrees.
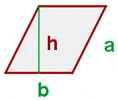
Area of Trapezoid
Trapezoid is a quadrilateral with one pair of parallel sides as shown in the figure below:

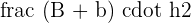
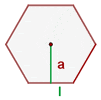
Area of a Regular Polygon
In geometry, a regular polygon is a polygon that is equilateral and equiangular. It means that all sides of the regular polygon are of the same length and all of its angles are of the same measure.
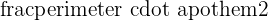
Polygon
If you have an irregular polygon which seems like the figure given below, then you can calculate the area by triangulating the polygon and adding the area of these triangles.


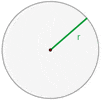
Circle
A circle is a geometrical figure in which all points are located at equal distance from its center.
 , where
, where 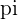 has a fixed value and "r" is the radius of the circle
has a fixed value and "r" is the radius of the circle
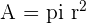 , where r is the radius of the circle
, where r is the radius of the circleCircular Sector
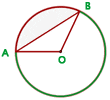
A circular sector, also referred to as a disk center or circle center is the portion of the circle that is enclosed by an arc and two radii of the circle.
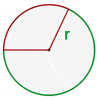
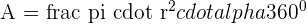
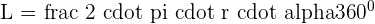
Circular Segment
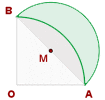
A circular segment refers to the region of the circle that is "cut off" from the remaining circle by a chord or secant.
The circular area of the segment AB = Area of the circular sector AOB - Area of triangle AOB
Lune of Hippocrates
It refers to the lune bounded by two arcs of the circle. You can read our article here to learn more about this concept.
Area of the lune = area of the semicircle − area of circular segment.
Area of the lune = Area of the right triangle
Circular Trapezoid
In two given concentric circle, a circular trapezoid refers to the area that lies between two non-crossing chords of the circle.


Area Enclosed between Two Concentric Circles
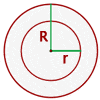

Surface Area and Volume Formulas
In this section of the article, we have compiled a list of surface area and volume formulas of various geometrical figures.
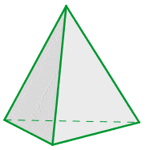
Tetrahedron
A tetrahedron refers to a solid that contains four plane triangular faces
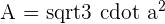

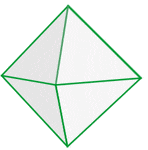
Octahedron
An octahedron refers to a three-dimensional shape which has eight plane faces.
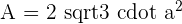
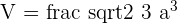
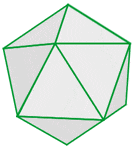
Icosahedron
Icosahedron refers to a solid figure that contains 20 plane faces.
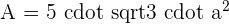
The formula for calculating the volume of the tetrahedron is:
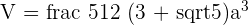
Dodecahedron
A dodecahedron refers to a three-dimensional figure with twelve plane faces.
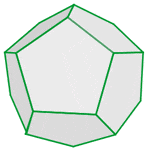

The formula for calculating the volume of the dodecahedron is:

Cube
A three-dimensional shape that contains six equal square is known as a cube.


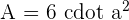
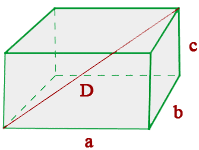
Cuboid
A three-dimensional geometrical figure that contains six rectangular faces is known as a cuboid
The formula for calculating the area of the cuboid is:

The formula for calculating the volume of the cuboid is:

Prism
A prism refers to a solid geometrical figure in which two ends are equal, similar and parallel rectilinear figures, and sides are parallelograms as shown in the figure below:
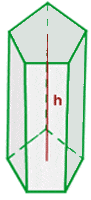
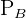 = Perimeter of the base
= Perimeter of the base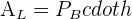


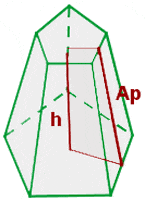
Pyramid
In geometry, a pyramid refers to polyhedron that is formed by joining the polygonal based an point, known as apex
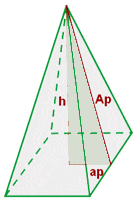
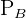 = Perimeter of the base
= Perimeter of the base
Ap = apothem of the pyramid
ap = apothem of the base
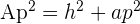
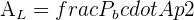


Truncated Pyramid
A truncated pyramid results from cutting a pyramid by a plane parallel to the base and segregating the portion that contains the apex.
P = Perimeter of the larger base
P' = Perimeter of the smaller base
A = Area of the larger base
A' = Area of the smaller base

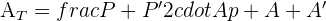

Cylinder
A cylinder as shown below refers to a surface that contains all the points on all the lines that are parallel to a given line and which pass through a fixed plane curve in a plane that is non-parallel to the given line.

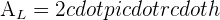
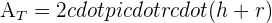
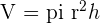
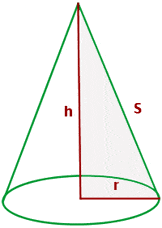
Cone
A cone in geometry refers to a three-dimensional shape that narrows smoothly from a flat base to a point known as a vertex or apex.

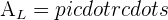

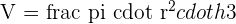
Truncated Cone
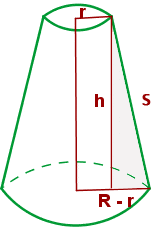
a cone section or pyramid lacking an apex and terminating in a plane usually parallel to the base.
It refers to the cone section or a pyramid that lacks an apex and terminates in a plane usually parallel to the base.
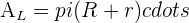
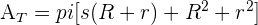
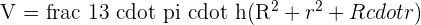
Sphere
Just like circle, a sphere refers to the set of points that are all located at the equal distance "r" from a given point.

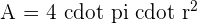

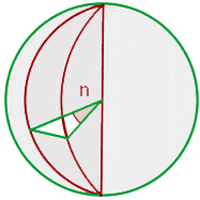
Spherical Wedge
A spherical wedge, also known as ungula is a part of a ball bounded by two plane semi disks and a spherical lune.

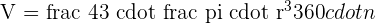
Spherical Cap
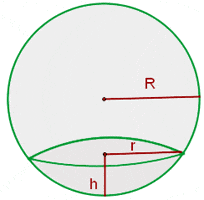
A spherical cap, also known as a spherical done is a part of sphere or a ball that is "cut off" by a plane.

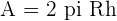

Spherical Segment
A spherical segment refers to a solid defined by cutting a ball or a sphere with a pair of parallel lines.

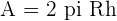
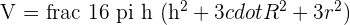
Summarise with AI:













Hi Emma nice to meet u I love reading and solving mathematics problem