Full circle, semi-circle, quarter circle, we all have gone through them but what if there is a random cut of a circle? Look at the below image.

A line cuts the circle into two unequal parts. What would be the name of both parts of the circle? There can be thousands of cuts like this, we can't name them all that is why mathematicians came up with a general name for all of them. They call it circular segments. A circular segment is an area of a circle that is enclosed by a chord and the corresponding arc. You might be wondering what is an arc and what is a chord? Let's talk about them.

Arc and Chord of a Circular Segment
We want you to check the first circle image again. There is some kind of irregularity. The green line doesn't make any sense. That is what we call a chord. A chord is a line that touches the border of a line on both ends but it doesn't pass through the centre of a circle. Usually, we deal with radius and diameter. They both have something in common and that is the centre of the circle. What if a line touches the border of a circle without passing through the centre of the circle? That is what we call a chord.
An arc is the border of a circle that is enclosed by diameter or radius. In the above example, there are two arcs. The first arc is the minor arc which is enclosed in the grey region. The other arc is the major arc that is denoted in the while region. Arc is just a shortcut of a circle boundary but it can't have 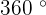 angle. That is the only condition, if the arc has
angle. That is the only condition, if the arc has 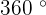 angle then it won't be an arc, it would be called a circle circumference.
angle then it won't be an arc, it would be called a circle circumference.
Area of a Circular Segment
Finding the area of a circular segment requires hard work. There is no direct formula to find the area of a circular segment because circular segments can be in any shape and size. That is why mathematicians came up with a trick. You can trick yourself by making that segment a circular sector and then find the area of the sector. Of course, that won't be enough, there will be a part that you need to subtract and that part shows to be a perfect triangle. Check the below circle for better clarification.
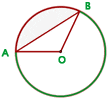
It is the same circular segment that we discussed above. What we did is transforming the circular segment into a circular sector. The sector consists of two shapes, one is the circular segment another is the triangle that is touching the centre. All you need to do is to find the area of the sector and then subtract it from the area of the triangle. In the above diagram, we have a sector AOB. We need to find the area of the circular segment, which is AB. Firstly, you will be finding the area of sector AOB and then find the area of the triangle AOB. Subtract the area of sector, AOB, from the area of the triangle, AOB, and you will get the area of the circular segment, AB.
The area of circular segment AB = area of the circular sector AOB - area of triangle AOB
Problems and Examples
A central angle of  is plotted on a circle with a 4 cm radius. Calculate the area of the circular segment enclosed by the chord joining the ends of the two radii and its corresponding arc.
is plotted on a circle with a 4 cm radius. Calculate the area of the circular segment enclosed by the chord joining the ends of the two radii and its corresponding arc.
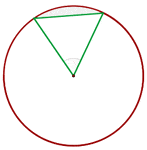
The area of circular segment = area of the circular sector - area of triangle
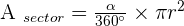
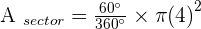
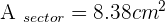
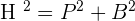

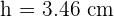
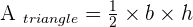
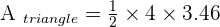

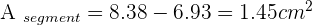
Find the area of the shaded portion of the square ABCD if  , and APC, AQC are centre circle arcs from their centre points B and D respectively.
, and APC, AQC are centre circle arcs from their centre points B and D respectively.
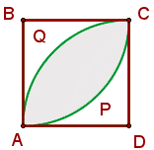
The shaded portion consists of two circular segments.
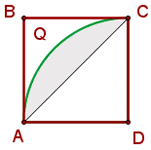

Calculate the area of both circular segments if the circular area of the segment = area of the circular sector − area of the triangle.
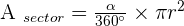

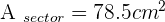
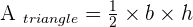
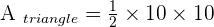
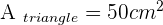















Hi Emma nice to meet u I love reading and solving mathematics problem