Chapters

Plane Definition
| Property 1 | A flat, two dimensional surface |
| Property 2 | It can extend forever in both directions |
| Property 3 | It has no thickness |
A plane is two-dimensional, which means that it only has two directions. Take a look at these directions below.

| Direction 1 | Up or down |
| Direction 2 | Left or right |
Plane Interactions
When you have a plane, you can have many different interactions within, or inside, that plane. In fact, a graph is an example of a plane, where you can have many different lines interacting with each other.

| Interaction 1 | Going in x or y directions |
| Interaction 2 | A point on a graph (x,y) |
| Interaction 3 | A line on a graph |
When you have more than one plane, you can have interactions between planes. These interactions are summarized in the table below.
| Interaction 1 | Intersecting | The planes intersect |
| Interaction 2 | Parallel | The planes are parallel to each other |
| Interaction 3 | Coincident | The planes are the same |
Take a look at these interactions in the images below.

| A | B | C |
| Intersecting | Parallel | Coincident |
Equation of a Plane
While a plane may be a two-dimensional surface, the plane itself is located in a three dimensional space. This may not make sense now, so let’s use an example. Say you have a sheet of paper in real-life.
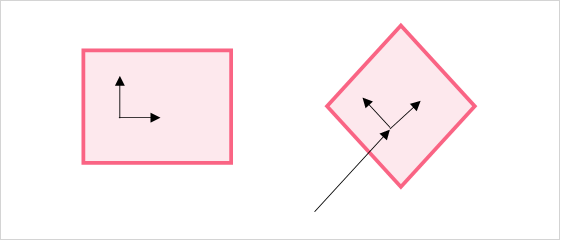
| A | Sheet of paper | Has two directions | Up or down and left or right |
| B | Paper in space | Has three directions | Up or down and left or right and tilt |
If you stick a pencil inside of a piece of paper, you can see that while the surface of the plane only has two directions, the plane itself can be moved around in any direction by that pencil. You can think of this pencil as the third direction of the plane.


| Equation | |
| Plane | Ax+By+Cz = D |
Intersection of Planes
Recall that intersecting planes mean that they cross each other. You should be careful when dealing with intersecting planes:
| Perpendicular | Intersection | |
| Meaning | Planes that intersect at a 90 degree angle | Planes that cross each other at any angle |
When you have two planes intersecting one another, you have a line that forms where they touch each other. Take a look below.

| Definition | |
| Line of intersection | The line where two planes meet |
As you can see, this line has a special name, called the line of intersection. In order to find where two planes meet, you have to find the equation of the line of intersection between the two planes.
System of Equations
In order to find the line of intersection, let’s take a look at an example of two planes. Let’s take a look at the equation of two planes, which are written in the table below.
| Plane 1 | Plane 2 | |
| Formula | 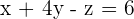 |  |
You can think of these two lines as a system of equations. A system of equations is defined in the table below.
| Definition | Notation | Example | |
| System of Equations | Two or more linear equations that have a relationship | The linear equations are written on top of one another | 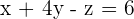
|
Parametric Form
When you have any line in space, you can write these linear equations in two ways:
- Parametric form
- Symmetric form
The easiest way to find the line of intersection is to work with the parametric form. The parametric form is defined in the table below.
| Definition | Parameter | |
| Parametric Form | The formula is written in terms of a parameter. |  |
In order to find the parametric form, we can use the system of equations from the previous section as an example and follow the steps in the table below.
| Step 1 | Solve the equations for one variable, like x | 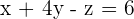 -> -> 
|
| Step 2 | Because the two equations equal to x, we can set them equal to each other | 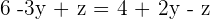 |
| Step 3 | Solve the equation for one variable, like z | 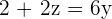 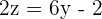
|
| Step 4 | Replace the equation for z into one of the original equations from step 1 |  -> ->  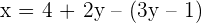 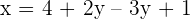
|
Finding the Line of Intersection
Now that we’ve followed the steps from the previous section, we have three equations.
| Equation 1 |  |
| Equation 2 | 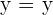 |
| Equation 3 | 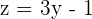 |
The equation for y is simply y = y. This is clear, because of course any given value for y is equal to itself. We could have done this for any of the other values (x=x, z=z).
Since they are all written in terms of the y value, all we have to do to get the equation of the line of intersection is replace these y terms with the parameter t. This gives us the parametric form of the line.
| Equation 1 | 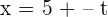 |
| Equation 2 |  |
| Equation 3 |  |
Together, these equations will give you any point on the line of intersection P(x,y,z).
Symmetric Form
If you want to have the line of intersection in symmetric form, you need to first find the parametric form of the line. Next, follow the two steps below.
| Step 1 | Set all equations for x, y and z in terms of the t parameter |
| Step 2 | Set all equations equal to each other |













Hi Emma nice to meet u I love reading and solving mathematics problem