
Introduction
In geometry, two of the most fundamental measurements we take of any shape are the perimeter and the area.
- Perimeter is the total distance around the outside of the shape. Think of it as the length of a fence needed to surround a field.
- Area is the amount of space enclosed within the shape. Think of it as the amount of grass needed to cover that field.
A polygon is simply any 2D shape with straight sides. While the method for finding the perimeter is usually the same (adding up the sides), the method for finding the area changes depending on the shape.
Perimeter of a Polygon
For almost every polygon, calculating the perimeter is straightforward. You simply find the sum of the lengths of all its outer sides.
For a regular polygon (where all sides are the same length), the formula is even simpler:
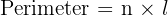
Where n is the number of sides and l is the length of one side.
Area of Triangles
The triangle is the simplest polygon. While there are different types of triangles (scalene, isosceles, equilateral), the general formula for area remains the same. We need the base (b) and the perpendicular height (h).
The formula for the area of a triangle is:
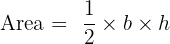
Area of Quadrilaterals
Quadrilaterals are polygons with four sides. Common examples include squares, rectangles, parallelograms, and trapeziums.
1. Square and Rectangle: For squares and rectangles, the area is the product of the length and width.
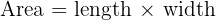
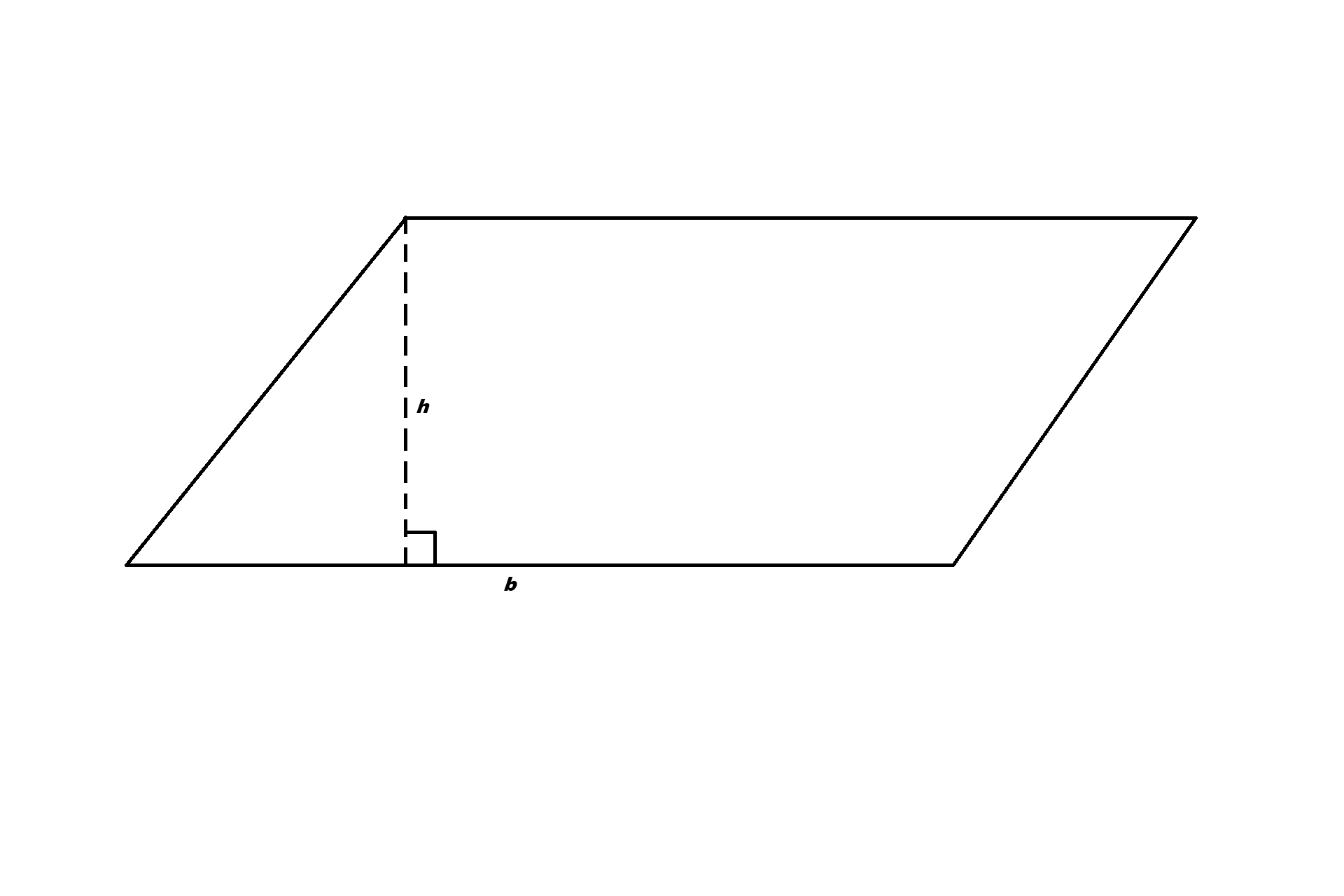
2. Parallelogram (Rhomboid): A parallelogram looks like a pushed-over rectangle. To find the area, we do not use the slanted side length; we must use the vertical height.
The formula is:
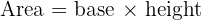
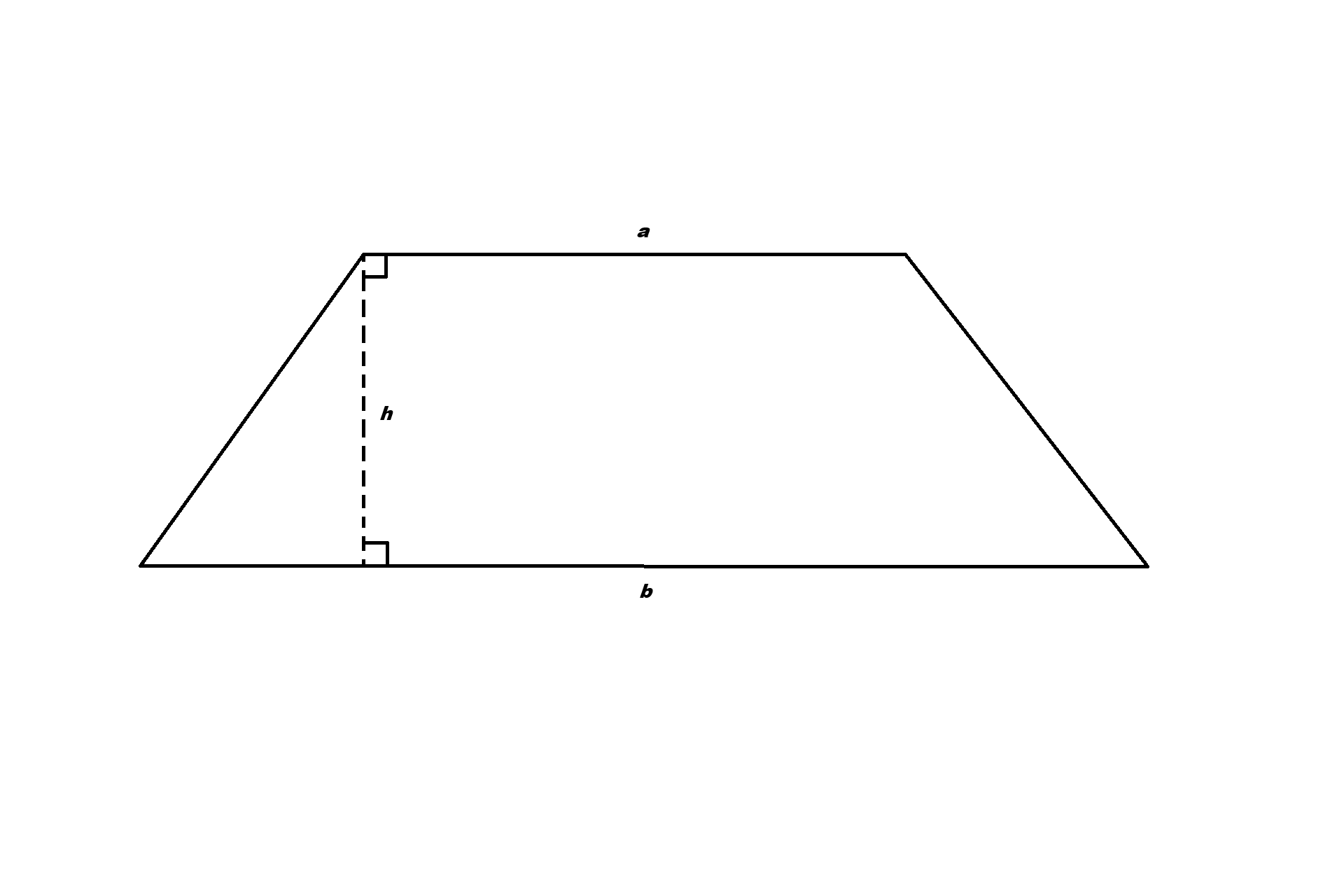
3. Trapezium (Trapezoid)
A trapezium has one pair of parallel sides. Let's call the lengths of these parallel sides a and b, and the distance between them h.
The formula is:
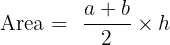
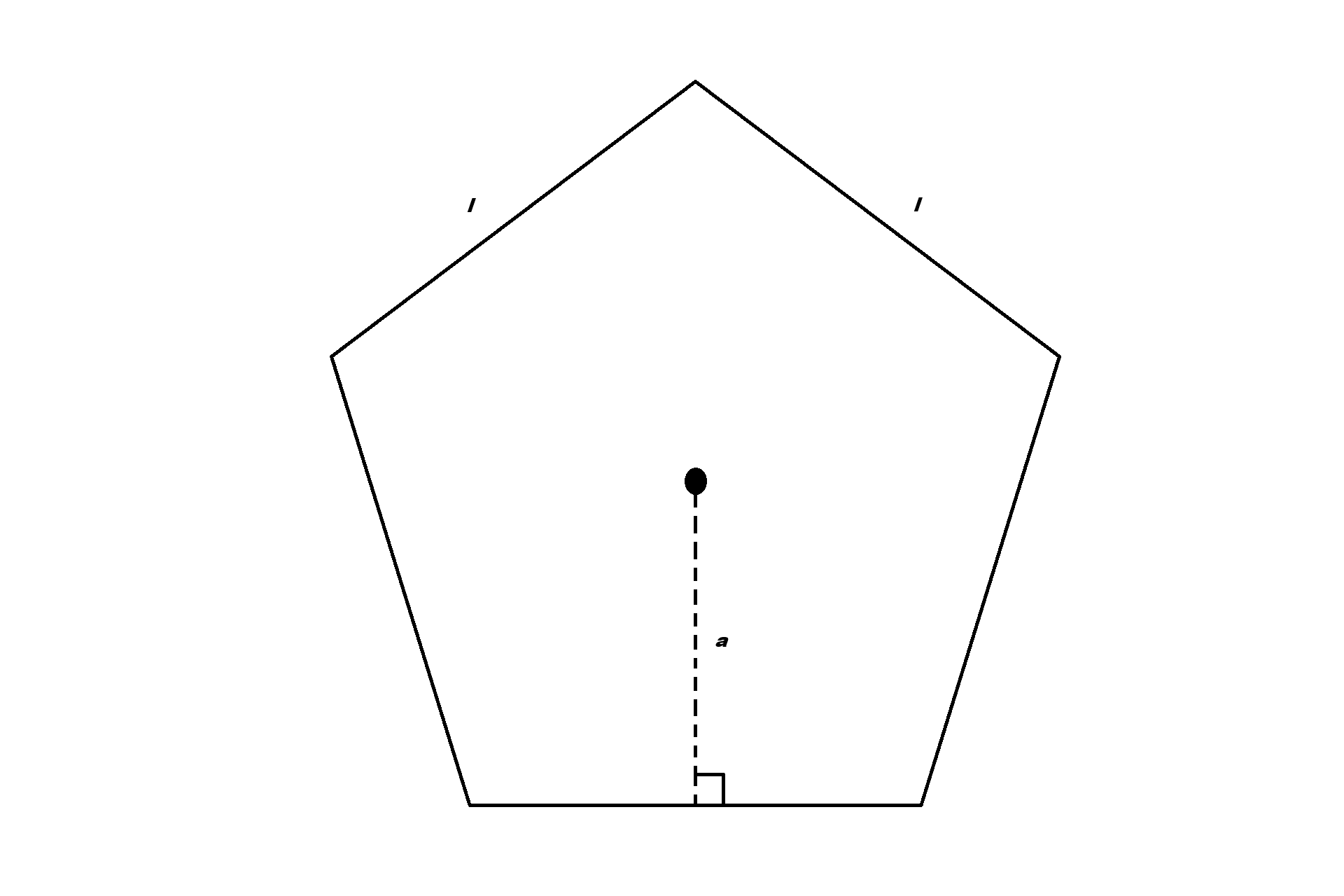
Area of Regular Polygons
A regular polygon has equal sides and equal interior angles (like a pentagon or hexagon).
To find the area, we use a special segment called the apothem (a). The apothem is the distance from the centre of the polygon to the midpoint of a side.
The formula uses the Perimeter (P) and the apothem (a):
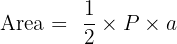
Practice Questions & Solutions
A rectangle has a length of 12 cm and a width of 5 cm. Calculate its perimeter and area.
To find the perimeter, we add all four sides (two lengths and two widths). Perimeter:
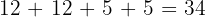
To find the area, we multiply the length by the width:
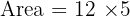
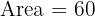
Answer: Perimeter = 34 cm, Area = 60 cm²
Calculate the area of a triangle with a base of 15 cm and a perpendicular height of 8 cm.
We use the standard formula for the area of a triangle:
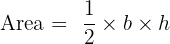
Substitute the values (b=15, h=8):
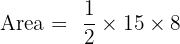
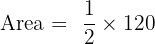
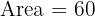
Answer: Area = 60 cm²
A trapezium has parallel sides of length 10 m and 16 m. The perpendicular height between them is 5 m. Calculate the area.
We identify the variables: a = 10, b = 16, and h = 5.
We use the trapezium area formula:
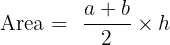
Substitute the values:
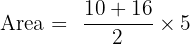
Calculate the sum in the numerator first:
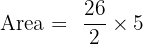
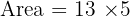
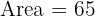
Answer: Area = 65 m²
A parallelogram has a base of 20 cm and a perpendicular height of 9 cm. The slanted side length is 11 cm. Calculate the area and the perimeter.
To find the area, we must use the base and the perpendicular height (not the slanted side). Area:
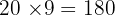
To find the perimeter, we add the lengths of the outer boundaries. A parallelogram has two pairs of equal opposite sides. Perimeter:
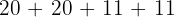
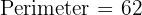
Answer: Area = 180 cm², Perimeter = 62 cm
A regular hexagon has a side length of 6 cm. The distance from the centre to the midpoint of a side (the apothem) is 5.2 cm. Calculate the area of the hexagon.
First, we must find the perimeter (P) of the hexagon. A hexagon has 6 sides, and each side is 6 cm.
Perimeter:
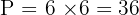
Now we use the formula for the area of a regular polygon using the apothem (a = 5.2):
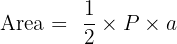
Substitute the values:
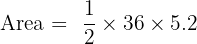
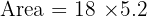
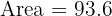
Answer: Area = 93.6 cm²












Hi Emma nice to meet u I love reading and solving mathematics problem