Chapters

Definition of a Polygon
| Definition | |
| Polygon | A polygon is a 2-dimensional shape that has 3 lines or more. Polygon is the main family for many different types of shapes. |
While we may not use the term polygon often to describe shapes in everyday life, the majority of the shapes we see everyday are polygons. Take a look at some examples below.
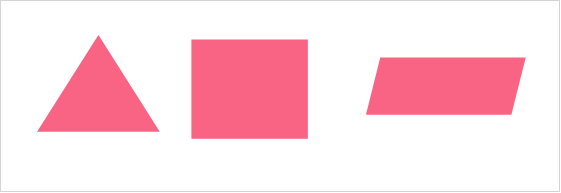
Types of Polygons
In the previous section, we defined what a polygon was. This definition, however, is quite broad – and there’s a reason for it. You can think of the term polygon as a term used to describe a group of different classifications for shapes. Let’s take a look at some of those groups.
| Polygons | |
| Group 1 | Quadrilateral |
| Group 2 | Parallelogram |
The two most common groups of shapes that are polygons are quadrilaterals and parallelograms. This might be getting confusing, so let’s simply start with what a polygon. Specifically, let’s take a look at what a polygon is not.

Take a look at the table below to see why it is not a polygon.
| Circle | |
| Two dimensional shape? | Yes |
| Has three lines or more? | No |
Quadrilaterals
Quadrilaterals are “under” the polygon definition. This means that all quadrilaterals are polygons, but not the other way around. This can be confusing, so let’s take a look at a comparison.

| A | B |
| All quadrilaterals are polygons but not all polygons are quadrilaterals | All dogs are animals but not all animals are dogs |
In order to understand what quadrilaterals are, let’s take a look at the three major properties that make a quadrilateral.
| Property 1 | A two dimensional figure |
| Property 2 | Made up of 4 line segments |
| Property 3 | Opposite sides are congruent |
As you can see, the first two properties are the exact properties that define what polygons are. However, the if a polygon also has the third property listed above, it is a special type of polygon called a quadrilateral.
Parallelogram
The other major type of polygon is called a parallelogram. Actually, a parallelogram is “under” the family of quadrilaterals. Similar to the way that quadrilaterals are a special type of polygon, parallelograms are a special type of quadrilateral.
Now, we have three levels of classifications for shapes.

| Rule 1 | All quadrilaterals are polygons but not all polygons are quadrilaterals |
| Rule 2 | All parallelograms are quadrilaterals but not all quadrilaterals are parallelograms |
You can think of these classifications as a hierarchy. Now, let’s take a look at the properties that all parallelograms have.
| Property 1 | A two dimensional figure |
| Property 2 | Made up of 4 line segments |
| Property 3 | Opposite sides are congruent |
| Property 4 | Opposite sides are parallel |
There are three types of parallelograms, all of which might be familiar to you. Take a look at them below.

Common Polygons
Now that you’re familiar with polygons and the different classifications under the polygon family, let’s take a look at the most common types of polygons. The five most common polygons are listed in the table below.
| 1 | Triangle | Polygon |
| 2 | Rectangle | Parallelogram |
| 3 | Square | Parallelogram |
| 4 | Rhombus | Parallelogram |
| 5 | Trapezium | Quadrilateral |
Each shape is classified by its “smallest” classification. Meaning, a triangle is classified as a polygon at most, while a square goes all the way down the classification hierarchy to parallelogram.
Naming Conventions
You may be wondering, how are polygons named? After all, we have seen some pretty odd names for types of polygons, such as parallelogram and quadrilateral. Let’s start with polygon itself. Take a look in the table below.
| Poly | Polygon |
| Many, much, one or more | Many sided shape |
The prefix poly- means many, which means that any shape that is a polygon has one or more sides. With some exceptions, such as the square, polygons are usually named by how many sides they have. Let’s take a look at some numbers and their corresponding prefixes.
| Number | Prefix |
| penta- | 5 |
| hexa- | 6 |
| hepta- | 7 |
| octa- | 8 |
| nona- | 9 |
| deca- | 10 |
| hendeca- | 11 |
| dodeca- | 12 |
No matter what subject you’re in - biology, chemistry, maths - these prefixes apply to anything. In math specifically, to get the name of a shape, you simply need to know these prefixes and the number of sides the shape has.
Polygons
As you saw in the previous section, all numbers have different prefixes. In order to get the name of a shape, you simply need to follow the rule in the table below.
| Prefix | -gon | Example | Meaning |
| Penta | -gon | Pentagon | 5 sided shape |
Now, let’s take a look at different polygons and see what they mean.
| Polygon | Meaning |
| Pentagon | 5 sided shape |
| Hexagon | 6 sided shape |
| Heptagon | 7 sided shape |
| Octagon | 8 sided shape |
| Nonagon | 9 sided shape |
| Decagon | 10 sided shape |
| Hendecagon | 11 sided shape |
| Dodecagon | 12 sided shape |
Now that you know what each shape means, as well as what their name means, let’s take a look at what these shapes actually look like.
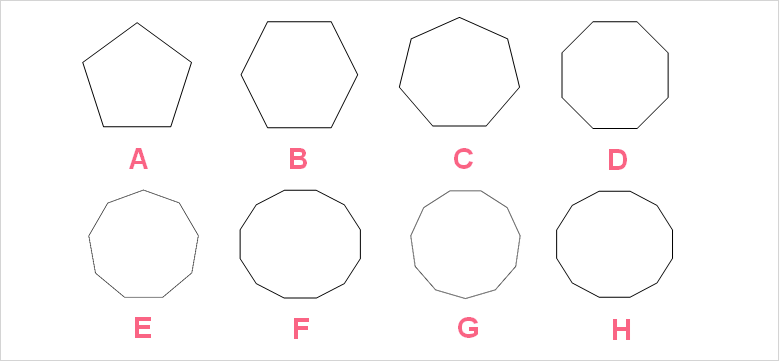
| Image | Polygon |
| A | Pentagon |
| B | Hexagon |
| C | Heptagon |
| D | Octagon |
| E | Nonagon |
| F | Decagon |
| G | Hendecagon |
| H | Dodecagon |
As you can see, polygons are fairly easy to remember if you know what the prefixes in their names mean.













Hi Emma nice to meet u I love reading and solving mathematics problem