
Introduction
From the wheels on a car to the orbits of planets, circles are one of the most fundamental shapes in the universe. In geometry, a circle is defined as the set of all points in a plane that are at a fixed distance from a central point.
To solve word problems involving circles, you need to be comfortable with a few key definitions and formulas:
- Radius (r): The distance from the centre to the edge.
- Diameter (d): The distance across the circle through the centre (d = 2r).
- Circumference (C): The distance around the edge of the circle (the perimeter).
- Area (A): The amount of space inside the circle.

Key Formulas
1. Circumference:
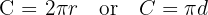
2. Area of a Circle:
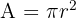
3. Length of an Arc:
An arc is a portion of the circumference. If the angle at the centre is theta:
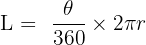
4. Area of a Sector:
A sector is a "slice of pizza" shape. The area is a fraction of the total circle:
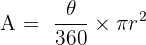
Practice Questions & Solutions
Anne is riding a horse which is tied to a pole with a 3.5 m piece of rope. Her friend Laura is riding a donkey which is 2 m from the same centre point. Calculate the distance travelled by each when they have rotated 50 times around the centre.
We need to calculate the circumference for each rider and multiply it by 50.
Anne (Radius = 3.5 m):
Calculate one rotation (circumference):
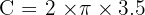
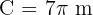
Multiply by 50 rotations:
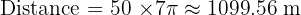
Laura (Radius = 2 m):
Calculate one rotation:
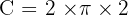
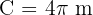
Multiply by 50 rotations:
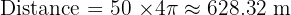
Answer:
Anne travels approx. 1099.56 m and Laura travels approx. 628.32 m.
The rope that attaches a swing to a tree is 1.8 m long. The maximum swing angle is 146 degrees. Calculate the maximum distance travelled by the seat of the swing (the arc length).
We are looking for the length of an arc.
Radius (r) = 1.8 m
Angle (degrees) = 146 degrees
Using the arc length formula:
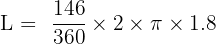
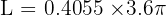
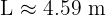
Find the area of a circular sector created by two radii connecting to the endpoints of a chord. This chord is the side of a square inscribed in a circle with a 4 cm radius.
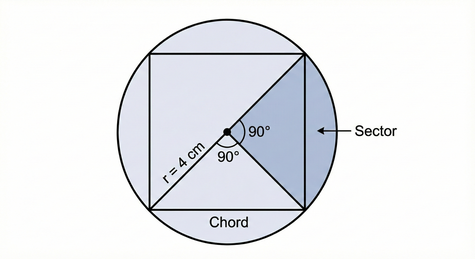
A square has 4 equal sides. If a square is inscribed in a circle, the 4 sides divide the circle into 4 equal parts. Therefore, the angle subtended by one side (the chord) at the centre is:
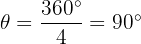
Now we find the area of the sector with r = 4 and theta = 90 degrees:
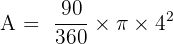
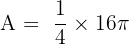
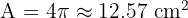
A circle with a radius of 3 cm is inscribed perfectly inside a square with a side length of 6 cm. Calculate the area of the shaded region (the space between the square and the circle).
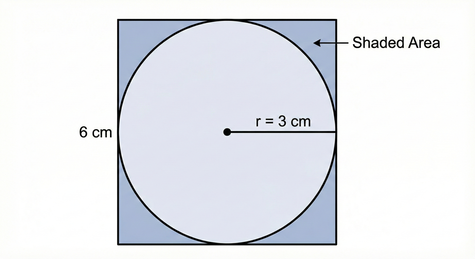
We must subtract the area of the circle from the area of the square.
1. Area of Square:

2. Area of Circle:
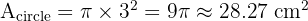
3. Shaded Area:
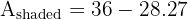
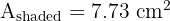
In a circular park with a radius of 250 m, there are 7 lamps. The base of each lamp is a circle with a radius of 1 m. The entire area of the park has grass except for the lamp bases. Calculate the lawn area.
We calculate the total park area and subtract the area of the 7 lamp bases.
1. Total Park Area:
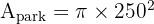
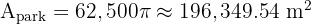
2. Area of 7 Lamps:
Area of one lamp base (r=1):
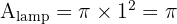
Total for 7 lamps:
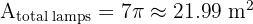
3. Lawn Area:
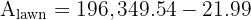
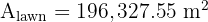
Two concentric circles (circles with the same centre) have radii of 8 cm and 5 cm. Two radii, OA and OB, form an angle of 60 degrees. Calculate the area of the circular trapezoid (the slice of the ring) formed between these radii.
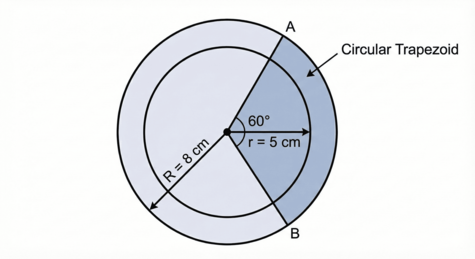
We need to calculate the area of the large sector (R=8) and subtract the area of the small sector (r=5).
1. Large Sector (R=8, theta=60):
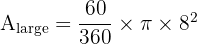
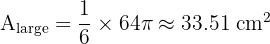
2. Small Sector (r=5, theta=60):
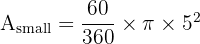
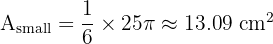
3. Trapezoid Area:
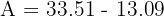
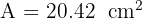
A circular fountain with a 5 m radius lies alone in the centre of a circular park with a 700 m radius. Calculate the total walking area available to pedestrians.
This is an annulus (a ring shape). We subtract the inner circle (fountain) from the outer circle (park).
1. Area of Park (R=700):
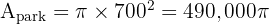
2. Area of Fountain (r=5):
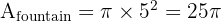
3. Walking Area:
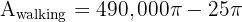
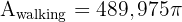
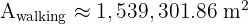
A central angle of 60 degrees is plotted on a circle with a 4 cm radius. Calculate the area of the circular segment (the region between the chord and the arc).
Area of Segment = Area of Sector - Area of Triangle.
1. Area of Sector:
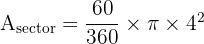
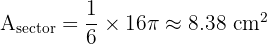
2. Area of Triangle:
Since the angle is 60 degrees and the two sides are radii (equal length), the triangle is equilateral.
Using the area formula for a triangle:
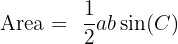
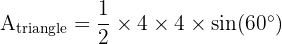
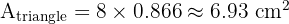
3. Area of Segment:
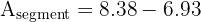
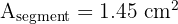
A chord of 48 cm is located 7 cm from the centre of a circle. Calculate the area of the circle.
To find the area, we first need the radius.
We can form a right-angled triangle where:
The height is the distance from the centre: 7 cm.
The base is half of the chord length: 24 cm.
The hypotenuse is the radius (r).
Using Pythagoras' Theorem:
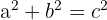
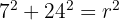
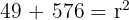
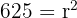
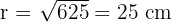
Now, calculate the area:
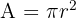
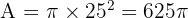
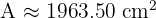
Calculate the area enclosed between the inscribed and circumscribed circles of a square with a diagonal of 8 m.
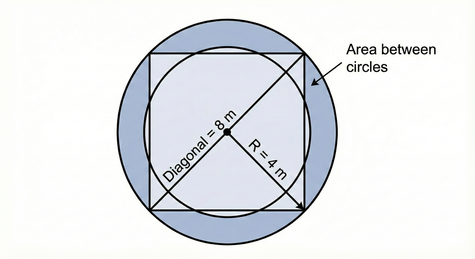
We need the area of the ring (annulus) formed by the outer circle and inner circle.
1. The Circumscribed (Outer) Circle:
The diameter of the outer circle is equal to the diagonal of the square.
Diameter (D) = 8 m.
Radius (R):
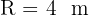
2. The Inscribed (Inner) Circle:
The diameter of the inner circle is equal to the side length of the square (s).
First, find the side length using Pythagoras on the square's diagonal:
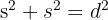
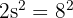
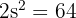
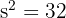
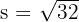
The radius (r) is half of the side length:
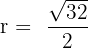
3. Area of the Ring:
We subtract the inner area from the outer area:
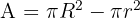
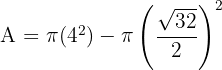
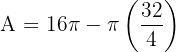
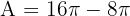
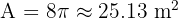












Hi Emma nice to meet u I love reading and solving mathematics problem