Chapters
In this article, we will see how to solve different types of probability word problems. But before proceeding to examples, let us define the probability first.

What is Probability?
Probability can be defined as:
The possibility of the occurrence of a random event
The formula for calculating the probability is given below:

The probability of a certain event is 1 and an impossible event is 0. The probability is always positive.
Example 1
There are 50 cookies in a box. Out of 50 cookies, 15 are chocolate-flavored, 20 are caramel-flavored, and the remaining are salted cookies. What is the probability of picking up:
a) a chocolate cookie randomly
b) a chocolate or caramel-flavored cookie
c) a chocolate and salted cookie
Solution
Part a
Number of chocolate-flavored cookies in a box = 15
Total number of cookies in a box = 50
Probability of picking up chocolate-flavored cookie = 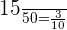
Part b
Number of chocolate-flavored cookies in a box = 15
Number of caramel-flavored cookies in a box = 20
Total number of cookies in a box = 50
Probability of picking up chocolate-flavored cookie = P(A) = 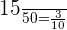
Probability of picking up a caramel-flavored cookie = P(B) = 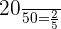
Probability of picking up a chocolate or caramel cookie = P(A) U P(B)
= 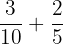
= 
Part c
Probability of picking up a chocolate cookie = P(A) = 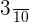
Probability of picking up a caramel= P(B) = 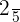
Probability of picking up a chocolate or caramel cookie= 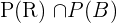
Both events are mutually exclusive, so the probability of picking up a chocolate and caramel cookie is 0.
Example 2
Solution
Part a
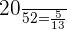
Part b

Part c

Example 3
Solution

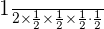
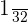
Example 4
Solution
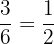


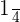
Example 5
In an area, 47% of the families own a car and a bike. 53% of the families own a car. What is the probability of a family owning a bike given that it already owns a car?
Solution
Percentage of the families who own both car and a bike = 47%
Probability of families owning a car and a bike= P(C and B) = 0.47
Percentage of families owning a car = 53%
The probability of families owning a car only = P(C) = 0.53
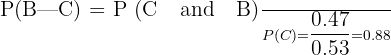
Example 5
Two dice are rolled simultaneously. What is the probability that the sum is:
a) less than 10
b) equal to 4
c) greater than 10
Solution
Part a
Total number of outcomes = 6 x 6 = 36
Sample space = S = { (1,1),(1,2),(1,3),(1,4),(1,5),(1,6), (2,1),(2,2),(2,3),(2,4),(2,5),(2,6), (3,1),(3,2),(3,3),(3,4),(3,5),(3,6), (4,1),(4,2), (4,3),(4,4),(4,5),(4,6), (5,1),(5,2),(5,3),(5,4),(5,5),(5,6), (6,1),(6,2),(6,3),(6,4),(6,5),(6,6) }
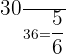
Part b
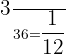
Part c
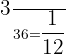
Example 6
What is the probability of selecting two prime number cards from the deck of 52 cards?
Solution
First, we will evaluate the types of cards present in each deck. A deck of 52 cards has the following attributes:
- There are four suits in a deck. Each suit has 13 cards
- Two of the four suits are black cards and two are red.
- The 13 cards in each suit include a king, a queen, a jack, ace, 2, 3, 4, 5, 6, 7, 8, 9, and 10.
In each suit, there are four prime numbers 2, 3, 5, and 7. Hence, in four suits, there will be 16 cards
Number of prime number cards in a deck = 16
Total number of cards in a deck = 52
The probability of selecting a prime number card from a deck = 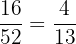
Now, we will calculate the probability of picking up the second prime number card from the deck.
Number of prime number cards left in a deck = 15
Total number of cards left in a deck = 51
The probability of drawing a prime number card, given a prime number card has already been drawn = 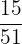
In this problem, we need to compute the probability of picking up two prime number cards, therefore we will multiply the probabilities we have calculated above:
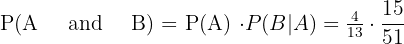
= 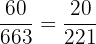
Example 7
Solution
Part a
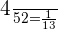
Part b
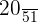
Part c














