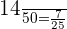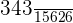Chapters
In this article, we will solve some examples related to probability. First, let us define probability:
The possibility of the occurrence of an event is known as probability
The probability of an event ranges from 0 to 1 and it is always a positive number. The probability of a certain event is 1 and the probability of an impossible event is 0. The formula for calculating the probability of an event A is given below:
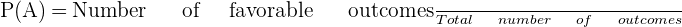

What is Conditional Probability?
Two types of events occur in our daily lives. These events are independent and dependent events.
a) Independent events: These events are not influenced by other events. For instance, when you toss a coin on the table. This event is not affected by any other event, hence it is known as an independent event. If we label the event as A, then its probability is written as P(A).
b) Dependent events: As the name depicts, these events are dependent on other events. Suppose you draw a card from a deck of 52 cards. Next time, you draw another card without replacement. Second time the total number of cards will be 51 instead of 52 because one card was already drawn. Hence, we can say that the second event is dependent on the first event.
A conditional probability refers to calculating the probability of an event that is dependent on another event.
We denote conditional probability like this:
P(A|B)
We use the following formula to calculate the conditional probability of two events A and B:

The formula can also be swapped according to the scenario in the question like this:

Now, we will solve couple of examples related to simple and conditional probability.
Example 1
What is the probability of selecting two red cards from the deck of 52 cards?
Solution
First, we will see the types of cards present in each deck.
- A deck has four suits.
- Two of the four suits are black cards and remaining are red.
- Each suit has 13 cards. The 13 cards include a king, a queen, a jack , ace, 2, 3, 4, 5, 6, 7, 8, 9 , and 10.
In a deck of 52 cards, there are 26 back cards. We need to select the two red cards from the deck, so, first, we will find the probability of selecting the first red card from the deck.
Number of red cards in a deck = 26
Total number of cards in a deck = 52
The probability of selecting a red card from a deck = 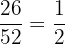
Now, we will calculate the probability of picking up the second red card from the deck.
Number of red cards left in a deck = 25
Total number of cards left in a deck = 51
The probability of drawing a red card, given a red card has already been drawn = 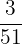
In this problem, we need to compute the probability of picking up two red cards, therefore we will multiply the probabilities we have calculated above:
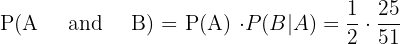
= 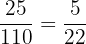
Example 2
There are 20 balls in the bag. 9 balls are green and the rest are blue. Three balls are drawn from the bag without replacement. What is the probability of drawing three blue balls from the pool?
Solution
First, we will calculate the probability of picking up the first ball.
Total number of balls in the bag = 20
Number of blue balls = 11
Probability that a randomly selected ball is blue = 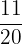
Now, we will calculate the probability of drawing the second ball.
Total number of balls left in the bag = 20 -1 = 19
Number of blue balls left in the bag = 11 - 1 = 10
Probability of selecting a blue ball second time = 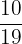
Now, we will calculate the probability of picking up a third blue ball.
Total number of balls left in the bag = 19 -1 = 18
Number of blue balls left in the bag = 10 - 1 = 9
Probability of picking up a blue ball third time = 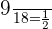
Probability of selecting three balls randomly of blue color = P(A) x P(B|A) = 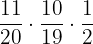
= 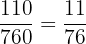
Example 3
From a deck of 52 cards, what is the probability of picking up a ace or number card?
Solution
Total number of cards in a deck = 52
Number of ace cards= 4
Probability of picking up a ace card = P(A) = 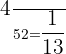
Number of numbered cards = 36
The probability of picking up a numbered card = P(N) = 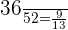
The probability of picking up a ace or a numbered card = P(A) U P(N)
=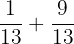
=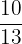
Example 4
In a class, 45% of the students play football and badminton. 55% of the students play football. What is the probability of a student playing badminton given he/she already plays football?
Solution
Percentage of the students who play football and badminton = 45%
Probability of students who play football and badminton = P(F and B) = 0.45
Percentage of students playing football = 55%
The probability of students playing football = P(S) = 0.55
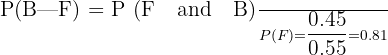
Example 5
Two dice are rolled simultaneously. What is the probability that the sum is:
a) equal to 6
b) less than 4
c) greater than 6
Solution
Part a
Total number of outcomes = 6 x 6 = 36
Sample space = S = { (1,1),(1,2),(1,3),(1,4),(1,5),(1,6), (2,1),(2,2),(2,3),(2,4),(2,5),(2,6), (3,1),(3,2),(3,3),(3,4),(3,5),(3,6), (4,1),(4,2), (4,3),(4,4),(4,5),(4,6), (5,1),(5,2),(5,3),(5,4),(5,5),(5,6), (6,1),(6,2),(6,3),(6,4),(6,5),(6,6) }

Part b
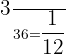
Part c
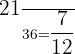
Example 6
Solution