Chapters

Probability
Random Variable
Random variables are distinct from traditional variables in many ways. A random variable can be defined as a variable whose outcomes are unknown. Check out the table below to compare random variables to traditional variables.
| Definition | Notation | Probability | Example | |
| Traditional | Outcome is known | x, y, b, a | No | Colour preference |
| Random | Outcome is unknown | X,Y,B,A | Yes | Height |
Random variables are different from traditional, algebraic values because their outcomes cannot be determined by one solution from an equation. The outcome of a random variable can only become known in the moment that the experiment or the event actually occurs.
Sample Space and Event
Let’s take the classic example of a coin toss as an example of a random variable. Let’s think about what we know about the outcomes of a coin toss.

We know that there are two outcomes: heads and tails. However, when we actually flip a coin, there is no way of knowing which outcome will occur until we check to see which side it has landed on. All possible outcomes of a random variable are defined as the sample space.

One or more outcomes in the sample space are called events. How many events are shown in the image above? The table below shows some possible answers.
| Notation | Explanation | |
| 1. | E(T) | Landing on tails |
| 2. | E(H) | Landing on heads |
| 3. | E(T,H) | First toss landing on tails, second toss heads |
Independent Event
In the table above, we gave several examples of events for a coin toss. The equation for the probability of an event is generalized below.

As you can see, for the 1st and 2nd rows in the table above, the probability for either event would be 0.50, or 50%. However, what happens when we want to calculate the probability of a combination of events happening, as in the 3rd row? The first step would be to determine what type of events they are.
| Definition | |
| Independent | The probability of one event does not depend on the outcome of another event |
| Mutually Exclusive (Disjoint) | Two events that cannot occur at the same time |
| Dependent | The probability of one event does depend on the outcome of another |
Let’s take a dice roll as an example of an independent event. You’re interested in the following.
| Notation | Explanation | |
| Sample Space | S = {1,2,3,4,5,6} | Can land on anything from 1 - 6 |
| Independent Event | E(1), E(2) | Land on 1, then land on 2 |
| Mutually Exclusive Event | E(1 and 2) | Land on 1 and land on 2 |
The probability of each event in the second row is  . This is because landing on 1 in the first roll does not affect whether or not we will roll 6 in the next. In fact, the probability of rolling each number is the same:
. This is because landing on 1 in the first roll does not affect whether or not we will roll 6 in the next. In fact, the probability of rolling each number is the same:  .
.
The probability of landing on 1 and 2 at the same time is zero. This is an example of a mutually exclusive event because, as you can see, it is impossible to land on both 1 and 2 on one roll.
Dependent Event
A dependent event, as we discussed earlier, is when the probability of one event depends on the outcome of another event. A classic example of a dependent event is selection without replacement.
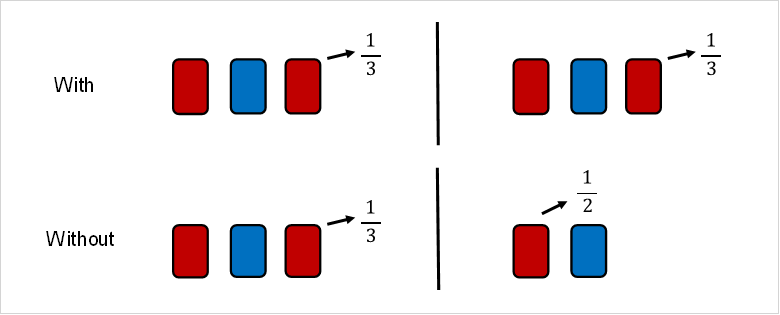
In the image above, selection with replacement is illustrated as the action of selecting something from the sample and putting it back after we’re done. This would be an independent event, as the probability before and after the colour is drawn is the same.
Selection without replacement, on the other hand, means that the probability of the same event, which is picking red, is different before and after the selection of a card.
Problem 1
This question will test your knowledge on different kinds of events. You have three different sets of information: one for sample A, sample B and sample C. Given the following information of the probabilities of each event, discuss which type of event we have. Keep in mind that each sample’s events are separate.
| Sample A | Sample B | Sample C | |
| E(X) | 1/3 | 1 | 1/3 |
| E(Y) | 1/3 | 0 | 2/3 |
| E(Z) | 1/3 | 0 | 0 |
Solution 1
Let’s take each sample separately.

In the first sample, each event has the same probability. This means that we are dealing with independent events.

In the second sample, we can see that if X happens then the probability of Y and Z are 0. This means these events are mutually exclusive events.

In the third sample, we can see each probability is different. This means that the events are dependent on each other.
Problem 2
There is a deck of 52 cards. There are the following cards included in the deck.
| Queen | 4 |
| Jack | 4 |
| Ace | 4 |
| King | 4 |
| 2 | 4 |
| 3 | 4 |
| 4 | 4 |
| 5 | 4 |
| 6 | 4 |
| 7 | 4 |
| 8 | 4 |
| 9 | 4 |
| 10 | 4 |
Find the probability of drawing a queen on the first draw and the second draw without replacement.
Solution 2
The image below simulates drawing 2 cards, one after the other, without replacement. First, we assume that a queen isn’t pulled the first draw.

As we can see, the probability on the first draw is 4 out of 52 cards. Because we don’t put this card back in the deck, our next draw is out of 51 cards. Also, because we haven’t drawn a queen, there are still 4 possible queens in the deck.
Next, we assume a queen is pulled on the first draw.

Here, because we drew a queen on the first draw, there are only 3 possible queens in the deck.
Problem 3
You are interested in the probability of rolling a dice. The events you are interested in are listed below.
| P(A) | Landing on 2 |
| P(B) | Landing on an even number |
Find the sample space and probabilities for each.
Solution 3
Find the solution in the table below.
| Event | Sample Space | Probability | |
| P(A) | Landing on 2 | S = {1,2,3,4,5,6} | 1/6 |
| P(B) | Landing on an even number | S = {2,4,6} | 3/6 = 1/2 |













