Chapters

Exercise 1
In a class in which all students practice at least one sport, 60% of students play soccer or basketball and 10% practice both sports. If there is also 60% that do not play soccer, calculate the probability that a student chosen at random from the class:
1 Plays soccer only.
2 Plays basketball only.
3 Plays only one of the sports.
4 Plays neither soccer nor basketball.
Exercise 2
In a city, 40% of the population have brown hair, 25% have brown eyes and 15% have both brown hair and eyes. A person is chosen at random.
1 If they have brown hair, what is the probability that they also have brown eyes?
2 If they have brown eyes, what is the probability of them not having brown hair?
3 What is the probability of them having neither brown hair nor brown eyes?
Exercise 3
There are two boxes. Box A contains 6 red balls and 4 blue balls and Box B contains 4 red balls and 8 blue balls. A die is rolled, if the number is less than 3, a ball is selected from box A. If the result is 3 or more, a ball is selected from Box B. Calculate:
1 The probability that the ball will be red and selected from Box B.
2 The probability that the ball will be blue.
Exercise 4
In order to write an exam, a student needs an alarm clock to wake up, which has proven to successfully wake him 80% of the time. If he hears the alarm in the morning the probability of writing the test is 0.9 and if he doesn´t hear the alarm the probability is 0.5.
1 If he writes the test what is the probability that he heard the alarm clock?
2 If he doesn´t write the test: what is the probability that he didn´t hear the alarm clock?
Exercise 5
On a shelf there are 60 novels and 20 poetry books. Person A chooses a book at random off the shelf and leaves with it. Shortly after, Person B chooses another book at random. Calculate:
1 The probability that the book selected by Person B is a novel?
2 If it is known that Person B chose a novel: what is the probability that the book selected by Person A was a poetry book?
Exercise 6
It is determined that 25 of every 100 men and 600 of every 1,000 women wear glasses. If the number of women in a particular room is four times more than that of men, calculate the probability of:
1 A person without glasses being randomly selected.
2 A woman with glasses being randomly selected.
Exercise 7
There are three sets of key rings A, B and C, for a house. The first set has five keys, the second has seven and the third has eight, of which only one key in each set opens the door to the store room. A keychain is chose at random followed by a key from the set.
1 What is the probability of the selected key being able to open the store room?
2 What is the probability that the chosen key chain is from the third set and the key does not open the door?
3 What is the probability that the chosen key opens the door and it came from the first key chain?
Solution of exercise 1
In a class in which all students practice at least one sport, 60% of students play soccer or basketball and 10% practice both sports. If there are 60% students who do not play soccer, calculate the probability that a student chosen at random from the class:
1 Plays soccer only.

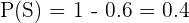
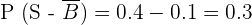
2 Plays basketball only.
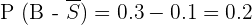
3 Plays only one of the sports

4 Plays neither soccer nor basketball
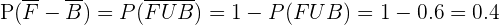
Solution of exercise 2
In a city, 40% of the population have brown hair, 25% have brown eyes and 15% have both brown hair and eyes. A person is chosen at random.
1 If they have brown hair, what is the probability that they also have brown eyes?
p (Brown eyes | Brown hair) = 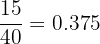
2 If they have brown eyes, what is the probability of them not having brown hair?
p (No brown hair | Brown eyes) = 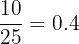
3 What is the probability of them having neither brown hair nor brown eyes?
p (neither brown hair or eyes) = 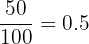
Solution of exercise 3
There are two boxes. Box A contains 6 red balls and 4 blue balls and Box B contains 4 red balls and 8 blue balls. A die is rolled, if the number is less than 3, a ball is selected from box A. If the result is 3 or more, a ball is selected from Box B. Calculate:
1 The probability that the ball will be red and selected from Box B.
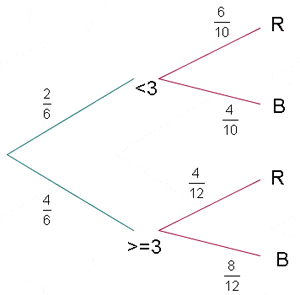
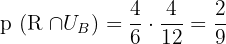
2 The probability that the ball will be blue.
p (Blue ball) = 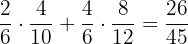
Solution of exercise 4
In order to write an exam, a student needs an alarm clock to wake up, which has proven to successfully wake him 80% of the time. If he hears the alarm in the morning the probability of writing the test is 0.9 and if he doesn´t hear the alarm the probability is 0.5.
1 If he writes the test what is the probability that he heard the alarm clock?

p (Heard |Test) = 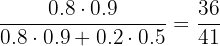
2 If he doesn´t write the test: what is the probability that he didn´t hear the alarm clock?
p (No heard|No test) = 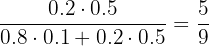
Solution of exercise 5
On a shelf there are 60 novels and 20 poetry books. Person A chooses a book at random off the shelf and leaves with it. Shortly after, Person B chooses another book at random. Calculate:
1 The probability that the book selected by Person B is a novel?

p (B novel) = 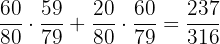
2 If it is known that Person B chose a novel: what is the probability that the book selected by Person A was a poetry book?
p (A poetry | B novel) = 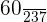
Solution of exercise 6
It is determined that 25 of every 100 men and 600 of every 1,000 women wear glasses. If the number of women in a particular room is four times more than that of men, calculate the probability of:
1 A person without glasses being randomly selected.

p (No glasses) = 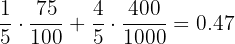
2 A woman with glasses being randomly selected.
p (Woman with glasses) = 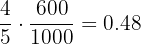
Solution of exercise 7
There are three sets of key rings A, B and C, for a house. The first set has five keys, the second has seven and the third has eight, of which only one key in each set opens the door to the store room. A keychain is chose at random followed by a key from the set.
1 What is the probability of the selected key being able to open the store room?

p (Open) = 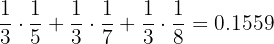
2 What is the probability that the chosen key chain is from the third set and the key does not open the door?
p (C and not open) = 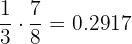
3 What is the probability that the chosen key opens the door and it came from the first key chain?
p (A|open) = 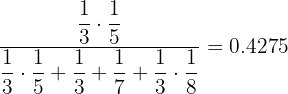













It is a vey good resources. I has a few problems of not showing parenthesis at the correct place. Those can be corrected easily.
Thank you so much for your feedback! 😊 We’re glad you found the resource helpful. We appreciate you pointing out the issue with the parentheses — we’ll review and fix those right away. Your input helps us keep improving!
Iam unable to understand
I specified that I wanted 7th-grader stuff but these are not even in my whole textbook
Someone relook at the examples. What z table are you referring to? Once you solve for the Z the rest of the answer is gibberish. Maybe sh o w the table, label the axes and red line the values you call out so the student can figure out what you are trying to convey.
Using facebook account,conduct a survey on the number of sport related activities your friends are involvedin.construct a probability distribution andbcompute the mean variance and standard deviation.indicate the number of your friends you surveyed
this page has a lot of advantage, those student who are going to be statitian