Chapters
In this article, we will discuss how bacteria become resistant to antibiotics as an example of natural selection. Furthermore, we will employ the Hardy–Weinberg principle to compute allele and genotype frequencies in populations and state the conditions when this principle can be applied.

Natural Selection: Antibiotic Resistance
We are often prescribed antibiotics by our healthcare professionals whenever we experience pathogenic bacterial infections. Antibiotics can be defined as:
The chemical substances that hamper or kill bacterial cells without causing any harm to human tissue
Derived from naturally occurring substances, antibiotics are dangerous to prokaryotic cells, however, they do not affect the eukaryotic cells. The main objective of antibiotics is to assist the immune system of the body in fighting a bacterial infection.
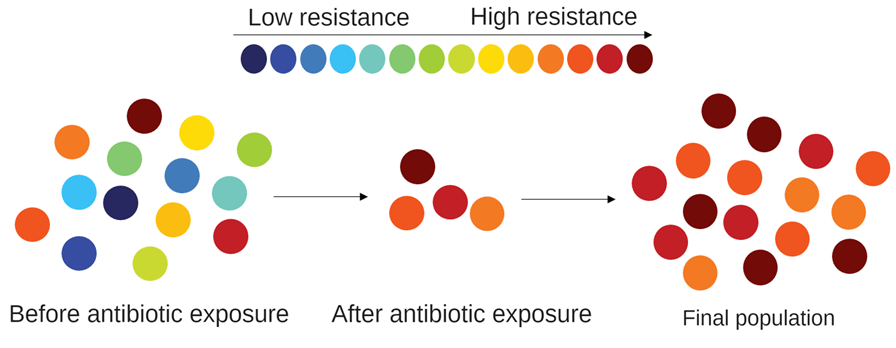
A popular example of an antibiotic is penicillin which was the first antibiotic that was discovered by Sir Alexander Fleming in 1928. We can categorize antibiotics either as bactericidal or bacteriostatic. Bactericidal antibiotics kill bacteria whereas bacteriostatic antibiotics inhibit their growth process. Like all other species, the diseases causing bacteria are genetically diverse. Some bacterial cells can have alleles that can be resistant to antibiotics. Random mutation generates these alleles which are not attributed to the use of antibiotics. Instead, they are caused by the selection pressures exerted by the antibiotics that lead to the increase in their frequency.
Bacteria contain a single loop of DNA with a single copy of each gene only so that with the rise of the new allele it is displayed in the phenotype immediately. In the presence of the antibiotic:
- Individuals possessing antibiotic-resistant alleles possess a great selective advantage. Hence, their chance of survival, reproduction, and passing their genome to the next generation is quite high.
- The chance of survival and reproduction of individuals without antibiotic-resistant alleles is quite low.
- Consequently, over many generations, the whole population of bacteria may become resistant to antibiotics.
One of the best examples of natural selection is antibiotic resistance.
What is the Future of Antibiotic Resistance?
The antibiotic-resistant strains are a matter of serious concern for scientists. The overuse of antibiotics is causing new strains to emerge rapidly. The overuse of antibiotics is exerting selection pressure on bacteria which is helping in the evolution of antibiotic resistance.
Scientists are facing a hard time discovering new antibiotics. However, the process of finding new antibiotics is costly and time-consuming. Few bacterial strains are resistant to multiple antibiotics and are creating diseases and infections that are hard to cure. With the discovery of antibiotics, the scientists were jubilant as they thought that now the bacterial infections will be eradicated, however, in the future, it is predicted that it would be impossible to treat several bacterial infections with current medicines.
Hardy-Weinberg Principle
According to the Hardy Weinberg principle, the allele frequencies of the gene within a population will not change from one generation to the next, if some specific conditions are fulfilled.
For the Hardy Weinberg principle to be true, the seven assumptions or conditions should be met. The Hardy-Weinberg equation enables us to compute the allele and genotype frequencies within populations. It also allows us to predict how these frequencies will change in future generations.
The Seven Conditions for the Hardy-Weinberg principle
Hardy Weinberg's principle assists in building models and making predictions. Hardy Weinberg's principle can only be applied to a population if the following series of conditions or assumptions are fulfilled:
- Organisms are diploid
- The reproduction of an organism occurs through sexual reproduction only
- No overlap between generations
- Random mating
- Large population
- No mutation, migration, or selection
- Allele frequencies are equal in both genders
Equations of Hardy Weinberg principle
If a single gene with only two alleles determines the phenotype of a characteristic in a population, then the population will have individuals with three possible genotypes. In this section, we will employ B/b as examples:
- Homozygous dominant (BB)
- Heterozygous (Bb)
- Homozygous recessive (bb)
While using the Hardy Weinberg equation, we represent frequencies as proportions (number out of 1) of a population. For instance, if each individual in a population possesses the homozygous dominant genotype BB, then its frequency will be 1. On the other hand, if half of the population exhibits this genotype, then the frequency will be 0.5.
We can represent the frequency of the alleles which is the proportion of all of the alleles in a population that has a specific form:
- The frequency of the dominant allele (B) is represented by the letter p
- The frequency of the recessive allele (b) is represented by the letter q
- Because there are just two alleles at a single locus for a phenotypic characteristic in the population, hence it means:
p + q = 1
For instance, a population having 100 individuals will have 200 alleles because each individual possesses two versions of each gene. If 120 out of 200 alleles were the dominant one, then the frequency of the dominant allele would be 120/200. We can say that:
p = 120/200 =0.6
If p = 0.6, then we can find q like this:
q = 1 – 0.6 = 0.4
We can also represent genotype frequencies which is the proportion of all the individuals with a specific genotype.
- The probability that an individual is homozygous dominant is p2. Since both, the parents will pass their dominant alleles to the offspring, hence p x p = p2
- The probability that an individual is heterozygous is 2pq. Either the father could pass on the dominant allele and the mother could pass on the recessive allele to the offspring p x q, or it could occur vice versa.
- The probability that an individual is homozygous recessive is q2. In this case, both parents can pass on their recessive alleles to the offspring, hence q x q = q2.
Since all these are possible genotypes of individuals in the population, so we can create the equation below:
p2 + q2 + 2pq = 1
Solved Example
Suppose in a population of birds 10% of individuals show a recessive phenotype of white feathers. What will be the frequencies of all genotypes?
We will use the letters F / f to represent the dominant and recessive alleles for the colour of the feather. Those possessing the recessive phenotype should contain the homozygous recessive genotype, ff. Hence, q2 = 0.10 because 10% of the individuals possess the recessive phenotype and it is represented by q2.
Follow these steps to compute the frequencies of the homozygous dominant p2 and heterozygous 2pq.
Step 1: Calculate q
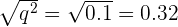
Step 2: Calculate p which is the frequency of the dominant allele F. Remember that q = 0.32, and p + q = 1.
p + q = 1
p = 1 - 0.32
p = 0.68
Step 3: Calculate p2 which refers to the frequency of the homozygous dominant genotype
0.682 = 0.46
p2 = 0.46
Step 4: Calculate 2pq = 2 x (p) x (q)
2 x (0.68) x (0.32) = 0.44
Step 5: Check your values by substituting the values for the three frequencies into the equation. Their aggregate should be equal to 1.
p2 + 2pq + q2 = 1
0.46 + 0.44 + 0.10 = 1
Summary of the Allele and Genotype Frequencies
Allele frequencies:
- p = F = 0.68
- q = f = 0.32
Genotype frequencies:
- p2= FF = 0.46
- q2= ff = 0.10
- 2pq= Ff = 0.44
Summarise with AI:













Keep on teaching us,you are excellent teachers
This is great
Thanks a lot for this book,it really helped me a lot
It’s useful to me
Thanks a lot for your Better book!
It’s a perfect article, go ahead