The words "Absolute" and "Relative" have a lot of meaning and domain in the world of Mathematics and Physics. Many laws and theories are developed concerning these concepts such as the theory of relativity, time dilation, velocity, etc. They are connected through the "Frame of reference" concept. Hence, before we start explaining to you the absolute and relative maxima and minima, we want to give you a small introduction to "Frame of Reference". If you are familiar with this then we would advise you to skip to the main topic.

Frame of Reference
To understand this concept, imagine you are standing still on a side of a road and you saw a car that went past you. The car was moving at a speed of 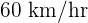 . You will notice that the car instantaneously vanished from your sight. From your point, you will say that the car was moving at a speed of
. You will notice that the car instantaneously vanished from your sight. From your point, you will say that the car was moving at a speed of 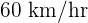 .
.
This time you are travelling in a car that is moving at a speed of 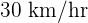 and the same car again ran past you again with the same speed
and the same car again ran past you again with the same speed 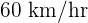 . This time, you will notice the car won't vanish instantaneously but at some time, it will take some time to vanish. You did some calculations and found that the car was moving at a speed of
. This time, you will notice the car won't vanish instantaneously but at some time, it will take some time to vanish. You did some calculations and found that the car was moving at a speed of 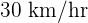 .
.
Now, your car and the same car started at the same time and your car's speed matched the speed of the other car (which is 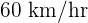 ). This time the car stays side by side, neither your car is leading nor the other car is leading. From your point, the speed of that car would be
). This time the car stays side by side, neither your car is leading nor the other car is leading. From your point, the speed of that car would be  .
.
Let's do some analysis. In the first scenario, you were stationary while the car was moving at a speed of 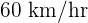 and, in fact, from your perspective, the car was moving at a speed of
and, in fact, from your perspective, the car was moving at a speed of 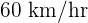 . We call this scenario absolute. This is because what you figured is the real speed of that car.
. We call this scenario absolute. This is because what you figured is the real speed of that car.
On the other hand, the car speed changed in the other two scenarios because you were also moving. The speed of the other car now depends on the speed of your car. For example, in the second scenario, the car was still going to overtake your car, but the same car with the same speed can't overtake your car in the third scenario. We call it relative motion. It means that we don't know the actual speed of that car but what we know is that the car was moving at a speed of 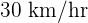 from your perspective (in scenario two). However, in scenario three, the car was stationary according to your perspective. The values noted will be relative to your motion and the beauty of this concept is that it can change. Let's say your car is moving at a speed of
from your perspective (in scenario two). However, in scenario three, the car was stationary according to your perspective. The values noted will be relative to your motion and the beauty of this concept is that it can change. Let's say your car is moving at a speed of 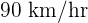 and the other car is moving at a speed of
and the other car is moving at a speed of 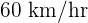 , you will notice that the car is moving back but in reality, the car is moving forward but you are too fast to observe it.
, you will notice that the car is moving back but in reality, the car is moving forward but you are too fast to observe it.
Absolute Maximum
Since you know what is absolute and what is relative, it is time to understand the concept of Absolute Maxima and Absolute Minima. A function has its absolute maximum at  if the ordinate is greater than or equal to any point in the domain of the function.
if the ordinate is greater than or equal to any point in the domain of the function.

If we analyze the above graph, the domain starts from zero and goes to negative infinity. Your goal is to find the highest ordinate value of the function and that would be your absolute maxima. The maximum value of ordinate that we get is when  , hence, we can conclude that the absolute maximum point of this function is at
, hence, we can conclude that the absolute maximum point of this function is at 
Absolute Minimum
A function has its absolute minimum at x = b if the ordinate is less than or equal to any point in the domain of the function.
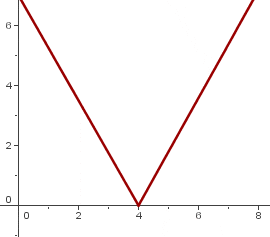
Since we are talking about the minimum, our goal would be to find the smallest ordinate value.

Relative Maximum and Minimum
Since you all know what does relative means, now you can understand what relative maximum and relative minimum mean. The term, relative maximum, means that the point is maximum but it is according to the points near it. That is why we say that the point, a, is maximum relative to the points near it. In the below graph, we can say that the relative maximum would be at  because at this point, we are getting the highest value of ordinate, which is
because at this point, we are getting the highest value of ordinate, which is  , relative to points near it. In short, a function, f, has a relative maximum at point, a, if f(a) is greater than or equal to the points near point a.
, relative to points near it. In short, a function, f, has a relative maximum at point, a, if f(a) is greater than or equal to the points near point a.
The same goes for relative minimum as well but the only difference is that the relative minimum will give you a minimum point relative to points near it. In the case of below graph, the relative minimum is at 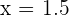 for which the value of the function is
for which the value of the function is  . In other words, a function, f, has a relative minimum at point b if f(b) is less than or equal to the points close to point b.
. In other words, a function, f, has a relative minimum at point b if f(b) is less than or equal to the points close to point b.

Summarise with AI:













I have math qstn problm
Break even point