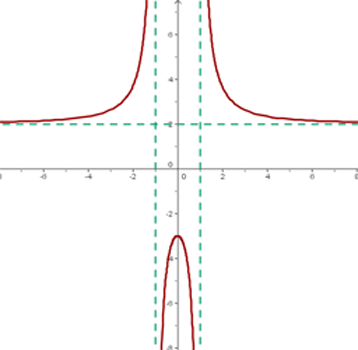
The asymptotes are straight lines on a graph that a function approaches indefinitely. You will find asymptotes with a curve only. In simple words, an asymptote is a straight line that approaches a curve but they both never meets each other. They both keep moving to infinity and since asymptote and the curve doesn't meet, it also means that asymptote doesn't overtake the curve and vice versa. There are three types of asymptotes:
- Horizontal Asymptotes
- Vertical Asymptotes
- Oblique Asymptotes

Horizontal Asymptotes
When the asymptote (asymptote parallel to the x-axis) reaches  or
or 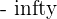 without touching the curve but approaching it at some point (let's call it "k"), we call it Horizontal Asymptote.
without touching the curve but approaching it at some point (let's call it "k"), we call it Horizontal Asymptote.
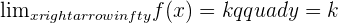

Vertical Asymptotes
If the x remains constant, however, the y approaches the curve but does not touches it as well as reaches infinity, the line will be called Vertical Asymptote


Oblique asymptote
Last but not least, the x moves to infinity and the equation of the line is  and the curve approaches that line, we will call it Oblique Asymptote.
and the curve approaches that line, we will call it Oblique Asymptote.
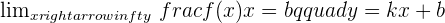

Example
Q. Calculate the horizontal asymptote of the function:


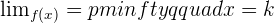
K are the points outside the domain of the function (in the rational functions).
Q. Calculate the horizontal and vertical asymptotes of the function:




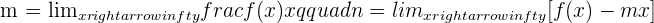
The oblique asymptotes will only be found when there are no horizontal asymptotes.
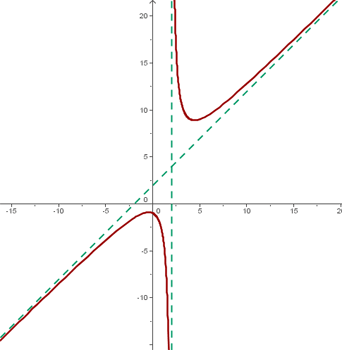
Q. Calculate the asymptotes of the function:

HORIZONTAL ASYMPTOTES

No horizontal asymptotes
VERTICAL ASYMPTOTES
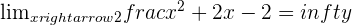

OBLIQUE ASYMPTOTES


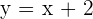













I have math qstn problm
Break even point