You will be familiar with derivatives which are the basis of differential calculus. The process of finding derivative of a function is known as differentiation. A derivative of a function shows instantaneous rate of change of a function at a given point. A derivative of the function f (x) is denoted by f ' (x).
In this article, we will discuss one of the crucial theoretical tools of calculus the "Mean Value Theorem" (MVT).

What is Mean Value Theorem?
One of the most important theories in Calculus is the Mean Value Theorem. According to this theorem,
If the function
is defined and continuous on a closed interval
and it can also be differentiated on
, then the interval
has at least one number c
in it in such a way that:
The geometric interpretation of the Mean Value Theorem tells us that there is a point where the tangent is parallel to the secant.
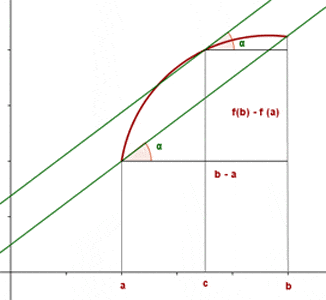
The unique case in which  is referred to as a Rolle's Theorem. In this case,
is referred to as a Rolle's Theorem. In this case, 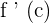 will be equal to 0.
will be equal to 0.
In the next section, we will use the mean value theorem to solve some problems.
Example 1
Find all the numbers c that satisfy the conclusion of the Mean Value theorem for the function below:
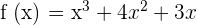 on
on 
Solution
We can immediately tell that the above function is a continuous function and is differentiable because it is a polynomial. Being differentiable means that the derivative of the above function exists at the closed interval  .
.
In the first step, we will find the derivative of a function 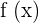 . This will be accomplished by using the rules of derivatives such as sum/difference and power rules:
. This will be accomplished by using the rules of derivatives such as sum/difference and power rules:

Now, in the next step, we will substitute the numbers of the interval in the following equation:
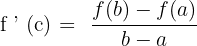
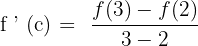
First, let us substitute 3 in the original function to get 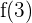 :
:
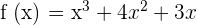


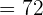
Now, let us substitute 2 in the original function to get 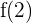 :
:
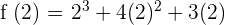
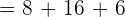

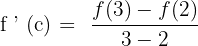
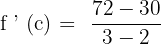
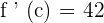
Now, we have got the following quadratic equation:

Replace x by c:
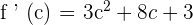
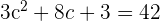
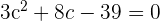
Note that the above equation is a quadratic one, so we can find the values of c using the following quadratic formula:
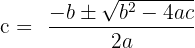
Here, a = 3, b = 8 and c = -39:
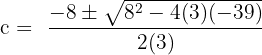
 and
and 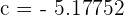
Note that we have got two values of c after substituting the values in a quadratic formula. One value  falls in the closed interval [2, 3], while the other negative value doesn't. This means that we will exclude the negative value of c. So, the only number which satisfies the mean value theorem is 2.51085.
falls in the closed interval [2, 3], while the other negative value doesn't. This means that we will exclude the negative value of c. So, the only number which satisfies the mean value theorem is 2.51085.
Example 2
Find all the numbers c that satisfy the conclusion of the Mean Value theorem for the function below:
 on
on 
Solution
We can immediately tell that the above function is continuous and differentiable because it is a polynomial. Being differentiable means that the derivative of the above function exists at the closed interval  .
.
In the first step, we will find the first derivative of the function 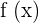 . This will be accomplished by using the rules of derivatives such as sum/difference and power rules:
. This will be accomplished by using the rules of derivatives such as sum/difference and power rules:

Now, in the next step, we will substitute the numbers of the interval in the following equation:
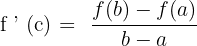
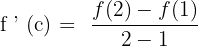
First, let us substitute 2 in the original function to get 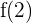 :
:

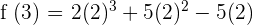
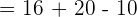
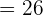
Now, let us substitute 1 in the original function to get  :
:
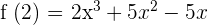

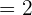
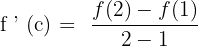
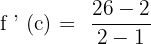
Simplify the above expression like this:
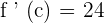
Now, we have got the following quadratic equation:

Replace x by c:


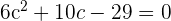
Note that the above equation is a quadratic one, so we can find the value of c using the following quadratic formula:
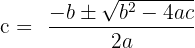
Here, a = 6, b = 10 and c = -29:
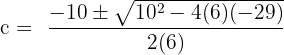
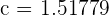 and
and 
Note that we have got two values of c after substituting the values in a quadratic formula. One value 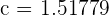 falls in the closed interval [1, 2], while the other negative value does not fall in the closed interval. This means that we will exclude the negative value of c. So, the only number which satisfies the mean value theorem is 1.51779.
falls in the closed interval [1, 2], while the other negative value does not fall in the closed interval. This means that we will exclude the negative value of c. So, the only number which satisfies the mean value theorem is 1.51779.
Example 3
Can the Mean Value Theorem be applied to 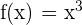 on [−1, 2]?
on [−1, 2]?
Solution
The function f(x) is continuous on [−1, 2] and differentiable on [−1, 2] so the Mean Value Theorem can be applied:
In the first step, we will find the derivative of the function 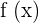 . This will be accomplished by using the derivative power rule:
. This will be accomplished by using the derivative power rule:
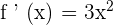
Now, in the next step, we will substitute the numbers of the interval in the following equation:
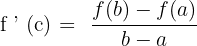
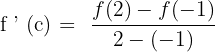
First, let us substitute 2 in the original function to get 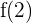 :
:


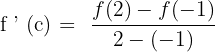
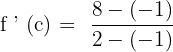

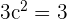
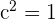
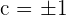
Hence, we have got two values of c 1 and -1. Both the values of -1 and 1 are part of the closed interval 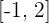 .
.
Example 4
Find all the numbers c that satisfy the conclusion of the Mean Value theorem for the function below:
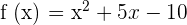 on
on 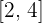
Solution
We can immediately tell that the above function is continuous and differentiable because it is a polynomial. Being differentiable means that the derivative of the above function exists at the closed interval 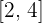 .
.
In the first step, we will find the derivative of the function 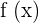 . This will be accomplished by using the rules of derivatives such as sum/difference and power rules:
. This will be accomplished by using the rules of derivatives such as sum/difference and power rules:
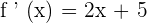
Now, in the next step, we will substitute the numbers of the interval in the following equation:
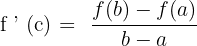
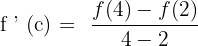
First, let us substitute 4 in the original function to get 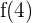 :
:
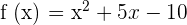

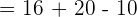
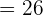
Now, let us substitute 2 in the original function to get 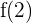 :
:
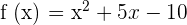
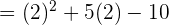
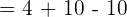
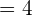
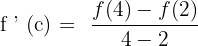
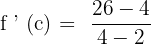
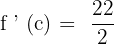
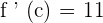
Now, we have got the following equation:
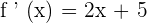
Replace x by c:
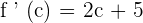
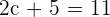
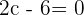
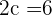

We have got only one value of c which is 3. 3 falls in the closed interval [2,4], hence it is the only answer to this problem.
Example 5
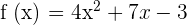 on
on 
Solution
We can immediately tell that the above function is continuous and differentiable because it is a polynomial. Being differentiable means that the derivative of the above function exists at the closed interval  .
.
In the first step, we will find the derivative of the function 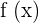 . This will be accomplished by using the rules of derivatives such as sum/difference and power rules:
. This will be accomplished by using the rules of derivatives such as sum/difference and power rules:

Now, in the next step, we will substitute the numbers of the interval in the following equation:
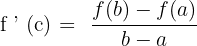
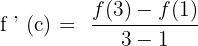
First, let us substitute 3 in the original function to get 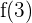 :
:
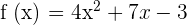

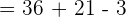
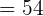
Now, let us substitute 1 in the original function to get  :
:
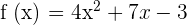



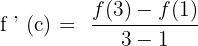
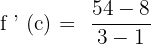
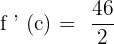
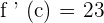
Now, we have got the following equation:

Replace x by c:
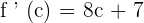

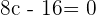
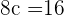

We have got only one value of c which is 2. 2 falls in the closed interval [1,3], hence it is the only answer to this problem.













I have math qstn problm
Break even point