The word quadratic is derived from a Latin word, "quadratum", which means square. As you guessed, any equation that has the degree of "2" is a quadratic equation. It is usually in the form of 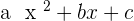 , where a, b, and c are constants. Let's analyze some equations, we have three equations and you need to identify which equations are quadratic and which not(with a reason).
, where a, b, and c are constants. Let's analyze some equations, we have three equations and you need to identify which equations are quadratic and which not(with a reason).
Take your time and find which equation/equations are quadratic or not. Here is the answer, the quadratic equations are on point number 2, and point number 4. The first equation contains 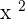 but it isn't a quadratic equation because it contains a higher power which is
but it isn't a quadratic equation because it contains a higher power which is 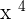 , hence the degree of this equation is "4" not "2". In the case of the third equation, the degree is "1" because it only has one variable whose power is one. Last but not least, the fifth equation has a problem. You can subtract both
, hence the degree of this equation is "4" not "2". In the case of the third equation, the degree is "1" because it only has one variable whose power is one. Last but not least, the fifth equation has a problem. You can subtract both 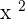 and you will be left with
and you will be left with 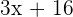 which is not a quadratic equation.
which is not a quadratic equation.
Let's draw a graph of a simple quadratic equation. Here is a quadratic equation, 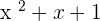 , now let's draw a graph.
, now let's draw a graph.
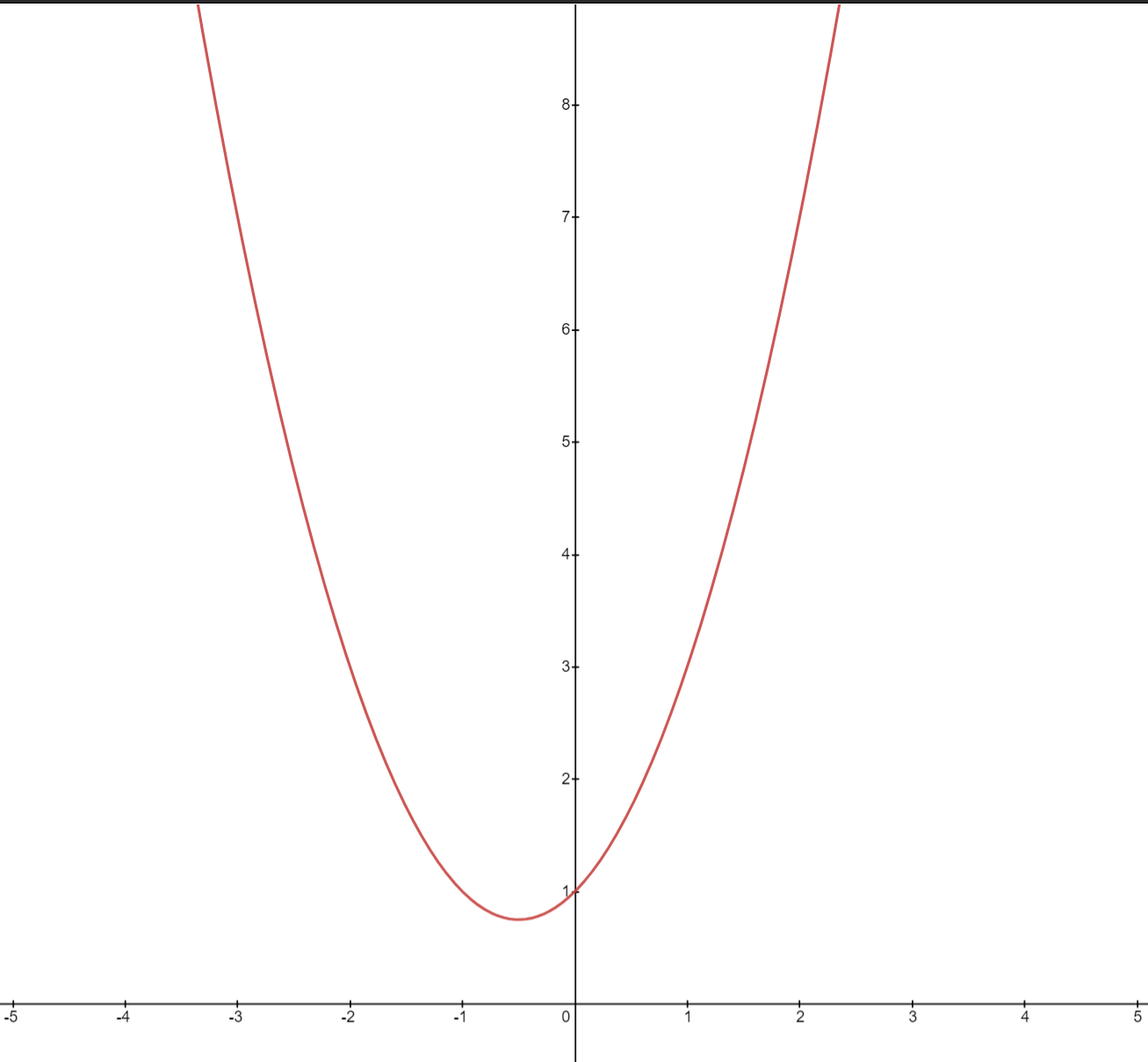
Does this graph look familiar with any shape to you? Yes! You are correct! It does look like a parabola. Can we conclude that all quadratic graphs look like a parabola? The answer is yes! Since the graph is a parabola, we will be applying all the rules and understandings of a parabola to it such as vertices, axis of symmetry, etc.

Graphical Representation of the Parabola
A parabola can be built from these points:
1. Vertex
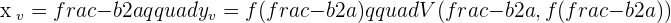
The axis of symmetry passes through the vertex of the parabola.
The equation of the axis of symmetry is:

2. x-intercepts
For the intercept with the x-axis, the second coordinate is always zero:
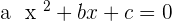
To find the x-intecepts, solve the resultant quadratic equation:
Two intercept points: 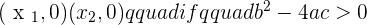
One intercept point: 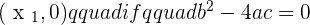
No intercept points if 
3. y-intercept
For the intercept with the y-axis, the first coordinate is always zero:
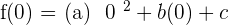

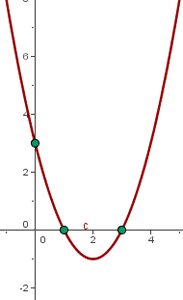
Example
Graph the quadratic function 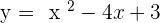 .
.
1. Vertex


2. x-intercepts
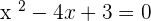
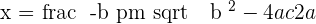

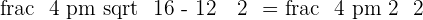
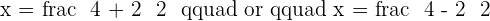
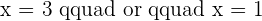
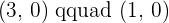
3. y-intercept
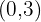
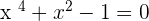
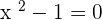
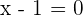
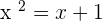













I have math qstn problm
Break even point