
Why Differentials Are Important?
Differentiation provides many pieces of information which are very helpful for many researchers. Sometimes, our focus is on finding a specific part, for that, we try to find short-cuts. For example, you have a quadratic equation and your point of interest is to understand whether the graph is concave or convex. The traditional way is to draw the whole graph and this will take a lot of your precious time. What if we told you that there is a way through which you can find whether the graph is concave or convex within just a few minutes? That is where differentials come in. In this lecture, we will talk about how you can find maximum, minimum, and inflection points with the help of derivatives.
To understand this lecture, you should know how to find derivatives of any equation. The type of equation doesn't matter here. It can be a polynomial equation, a linear equation, an exponential equation, whatsoever, what you need to know is what piece of information you will get after performing differentials. One of the biggest as well as common misunderstandings is that many students think that you can perform differentials just one time on any function. That is not true, you can perform as many differentials as you can on a function. Let's say you have a cubic equation, you can take at least three times differentials but after three times, the answer will become constant (i.e. 0). In that three times, the answer might be different and unique but after three times, the answer becomes constant.
Maxima, Minima, and Inflection Points
To understand easily, we made a small hierarchy.



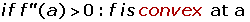
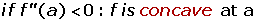
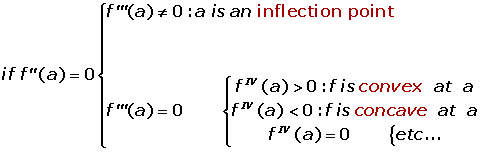
Let's understand what it means. If you take the first derivative of a function, it will give you a slope. In case, if you end up with an algebraic equation, you might need to enter the value of the variable to find the slope at that specific point. In addition, the first derivative also tells you whether the function is an increasing or decreasing function. If you take the second derivative of an equation, you can learn about the maximum or minimum point of the graph. If 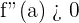 , it means your graph has a minimum point (which will obtain a "U" shape). On the other hand, If
, it means your graph has a minimum point (which will obtain a "U" shape). On the other hand, If 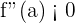 , it means your graph has a maximum point.
, it means your graph has a maximum point.
What happens if you take the third derivative of an equation? It will tell you about the same, minimum and maximum points relative to the first derivative. Furthermore, it also shows whether the function is increasing or decreasing. The simplest identification is that if the 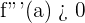 then the function is an increasing function and vise versa. Last but not least, the fourth derivative also talks about maxima and minima points but it also shows some more information than just telling you the maximum or minimum point.
then the function is an increasing function and vise versa. Last but not least, the fourth derivative also talks about maxima and minima points but it also shows some more information than just telling you the maximum or minimum point.
To find whether you are dealing with a convex or concave graph, you need to find whether the graph has a maximum point or minimum point. If the graph has a minimum point that means the function has a convex structure. On the other hand, if the graph has a maximum point, it indicates that the graph has a maximum point. Last but not least, if the third derivative is not equal to zero, it means that the graph has an inflection point but in case, if the third derivative becomes zero, it means the graph has no infection point.













I have math qstn problm
Break even point