Chapters

Monotone Sequence Definition

We can easily plot inequalities on a number line. Inequalities are operations that compare two or more numbers. Possible inequalities and their descriptions can be found in the table below.
| < | Less than | 2 < 5 |
| > | Greater than | 10 > 1 |
| = | Equal to | 4 = 4 |
 | Less than OR equal to | 5  5 5 |
 | Greater than OR equal to | 7  2 2 |


A monotone sequence is a special kind of sequence, where the number before it is either greater or less than the one before it. Take the following as an example.

Increasing Monotonic Sequence
A monotonic sequence can be either increasing or decreasing. When a monotonic sequence is increasing, each number is greater than the one that came before it. There are two types of increasing monotonic sequences:
- Weakly monotonic
- Strictly increasing
| Weakly monotonic | 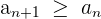 | Each number is greater than or equal to the one that came before it |
| Strictly increasing | 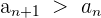 | Each number is greater than the one that came before it |
Let’s look at an example of each of the above types of increasing monotonic sequences.

As you can see, this is a weakly monotone increasing sequence because it is:
- Increasing with each number
- Each number is equal to or greater than the previous one

Decreasing Monotonic Sequence
A decreasing monotonic sequence is the exact opposite of an increasing monotonic sequence. One thing they have in common is that decreasing monotonic sequences can also be weakly or strictly decreasing.
| Weakly monotonic |  | Each number is less than or equal to the one that came before it |
| Strictly decreasing |  | Each number is less than the one that came before it |
An example of a weakly decreasing monotonic sequence can be seen below.

An example of a strictly decreasing monotonic sequence can be seen below.

Monotone Convergence Theorem
The monotone convergence theorem deals with monotonic sequences. In order for the theorem to work, we have to have three conditions, found in the table below.
| Condition 1 | Sequence 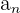 has to be a sequence with real numbers has to be a sequence with real numbers |
| Condition 2 | Sequence 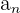 is increasing and bounded above is increasing and bounded above |
| Condition 3 | Sequence 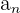 is decreasing and bounded below is decreasing and bounded below |
In other words, as the limit of the sequence increases towards infinity, it converges, or meets, some number.
Comparing Monotonic Sequences
Let’s take a look at some of the most common sequences and compare them. The table below defines each common sequence and gives an example.
| Arithmetic | The same number is added to the previous number each time | 3,13,23,33,43... |
| Geometric | The same number is multiplied to the previous number each time | 4,8,16,32,64... |
| Fibonacci | The two numbers before the first one are added together | 0,1,1,2,3,4,8,13... |
These special sequences are ones that you will probably encounter in any maths class. Let’s take a look at the arithmetic sequence first.
As you can see, we start with the number 3. Then, we add 10 to it, giving us 13. Next, we add 10 to that number, giving us 23. We can repeat this pattern to infinity. Now, let’s examine the geometric series.
Here, it is clear that we start with 4, multiply by two and get 8. Next, we multiply 8 by 2 and get 16; multiply 16 by 2 and get 32, etc.
Example 1
Come up with your own sequence. It can be:
- Weakly or strictly monotonic
- Increasing or decreasing
- A special sequence (arithmetic, geometric, Fibonacci)
Based on this task, we have given some examples of what your response may be.
| Weakly monotonic | 10, 10, 9, 9, 8, 8, 7, 7 |
| Strictly increasing | 1,3,4,7,9 |
| Strictly decreasing | 33,29,15,10 |
| Arithmetic | 101,102,103,104 |
| Geometric | 10,100,1000,10000 |
Example 2
Classify the following sequences as either weakly monotonic or strictly monotonic, as well as whether it is increasing or decreasing. Give an explanation to justify your answer.
- 10,9,8,7,6,5,4,3,2,1,0,-1,-2
- 3,3,4,5,6,6,7,8,9,10,10
- 4,4,4,4,4,4,4,4
The first sequence is strictly decreasing because each number is less than the one before it. The second sequence is weakly increasing, because each number is greater than or equal to the one before it. We can’t classify the third one, as the numbers are all equal to each other.
Example 3
Take the following sequence:
\[
1, 23, 45, 67, 89, 111, 133
\]
What is the pattern here?
The easiest way to find the pattern of a sequence is to first see whether each number is divisible by the previous one. As you can see below, we get a different number every time, which means it is not geometric.
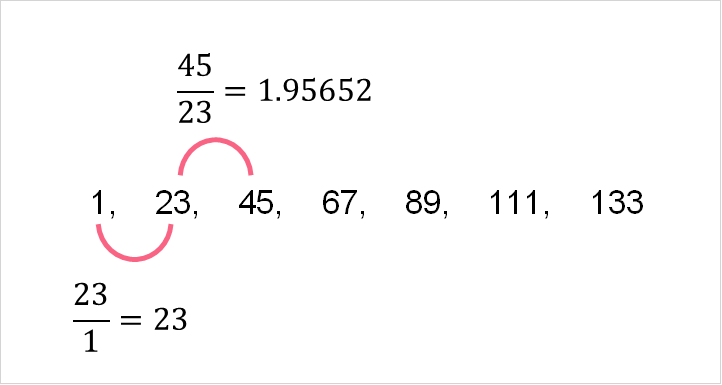
If this doesn’t work, try subtracting. This is an arithmetic sequence.
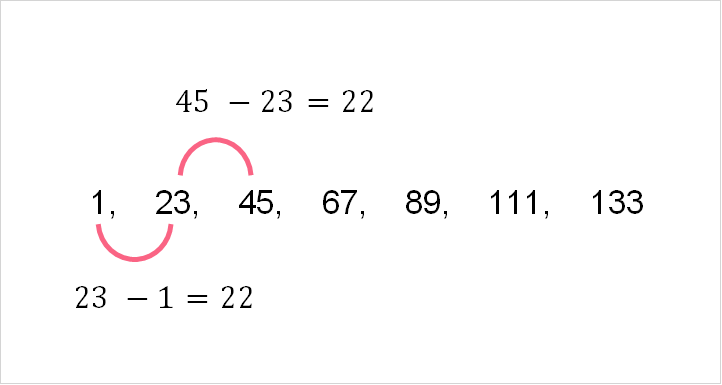
Summarise with AI:













I have math qstn problm
Break even point