Chapters
If there are two functions: f(x) and g(x), and the 2nd domain is within the range of the 1st, it can be defined as a new function that associates each element of the domain of f(x) with the value of g[f(x)].
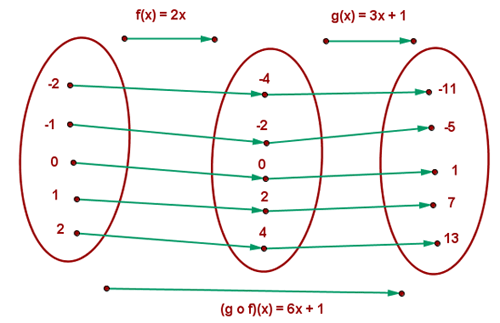
(g o f) (x) = g [f(x)] = g (2x) = 3 (2x) +1 = 6x + 1
(g o f) (1) = 6 · 1 + 1 = 7

The best Maths tutors available
Domain
D(g o f) = {x 
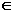
Properties
Associative:
f o (g o h) = (f o g) o h
Not commutative.
f o g ≠ g o f
The identity element is the identity function, i(x) = x.
f o i = i o f = f
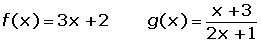

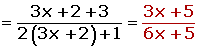




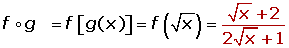
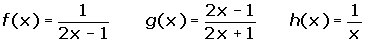
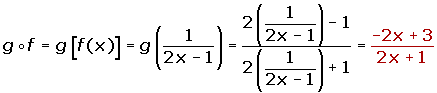
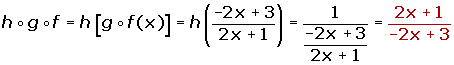













I have math qstn problm
Break even point