Chapters

What is a Periodic Function?
When we say that an object is in periodic motion, then we mean that the motion of an object is repeated after equal time intervals. Consider the examples of a swing that is in periodic motion because it repeats its motion after equal intervals of time. In mathematics, we define a periodic function as:
A function that gives the same value at regular intervals is known as a periodic function
Or
The function which repeats its values after regular intervals of time is known as a periodic function
We use periodic functions in science to explain the phenomenon of waves and oscillations etc. For example, have you ever observed waves of an ocean? They are often repeated after equal intervals of time. The time interval between the two waves is called a period. A function that is not periodic is known as an aperiodic function.
Mathematical Notation
A function, f(x), is periodic for period T, if it is verified for every integer (z):

Here T is a non-zero constant that is also known as a period of the function. A function having a period T will undergo repetitions on intervals of length T. These intervals are also called periods of a function.
Amplitude and Frequency of the Function
Consider the following graph of a periodic function.

The amplitude of the function is the distance from the trough or peak of the function to the line at the center. Consider the function 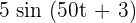 . In this function, the amplitude of the function is 3.
. In this function, the amplitude of the function is 3.
The frequency of the function shows that how many times it undergoes repetitions per unit of time. The frequency and period of the function are related to each other because we can derive frequency from period and period from frequency.
Period = 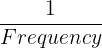
Frequency = 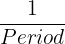
Periods of Trigonometric Functions
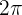 period as shown below:
period as shown below: sin (x + 2π) = sin x
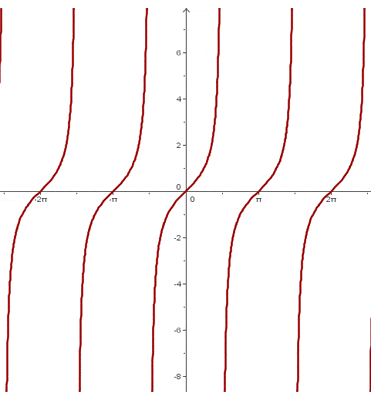
The function f(x) = tan x is periodic with period π.
tan (x + π) = tg x
Formula for Period of a Function
If there is a periodic function f(x) with period T, the function g(x) = f(kx) has a period of:
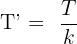
In the next section, we will solve some examples in which we will find periods of functions.
Example 1
Find the period of the following function:
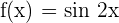
Solution
As we have discussed earlier that a period T of a periodic function f (x) is calculated using this formula:
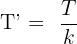
Since it is a sine function, hence it has period of 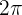 . So, T =
. So, T = 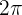 and
and 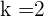 . Substitute these values on the above formula to get the value of T':
. Substitute these values on the above formula to get the value of T':
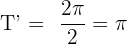
Hence, the period of the sin 2x is  .
.
Example 2
Find the period of the following tangent function:
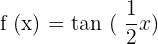
Solution
We know that the period of the tangent function 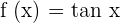 is
is  . So, the value of T is
. So, the value of T is  . Now, let us see what is the value of k. The function in this example is given in the form
. Now, let us see what is the value of k. The function in this example is given in the form 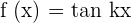 , where
, where 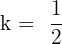 . We will substitute these values of T and k in the below formula to get the period of the function in this example:
. We will substitute these values of T and k in the below formula to get the period of the function in this example:
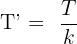

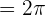
Hence, the period of the function 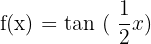 is
is 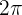
Example 3
Find the period of the following sine function:
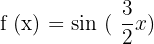
Solution
We know that the period of the sine function  is
is 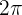 . So, the value of T is
. So, the value of T is 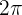 . Now, let us see what is the value of k. The function in this example is given in the form
. Now, let us see what is the value of k. The function in this example is given in the form 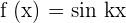 , where
, where 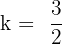 . We will substitute these values of T and k in the below formula to get the period of the function in this example:
. We will substitute these values of T and k in the below formula to get the period of the function in this example:
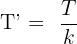
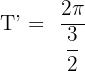
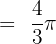
Hence, the period of the function 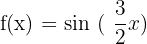 is
is 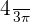 .
.
Example 4
Find the amplitude and period of the following function:
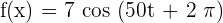
Solution
This function is given in the form  . Here, the value of the constant k is 50 and period of the function is
. Here, the value of the constant k is 50 and period of the function is  .
.
We will substitute these values of T and k in the below formula to get the period of the function in this example:
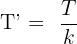
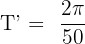
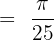
Hence, the period of the function 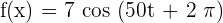 is
is 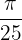 .
.
Example 5
Find the period of the following sine function:
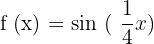
Solution
We know that the period of the sine function  is
is 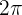 . So, the value of T is
. So, the value of T is 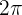 . Now, let us see what is the value of k. The function in this example is given in the form
. Now, let us see what is the value of k. The function in this example is given in the form 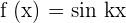 , where
, where 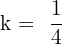 . We will substitute these values of T and k in the below formula to get the period of the function in this example:
. We will substitute these values of T and k in the below formula to get the period of the function in this example:
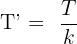
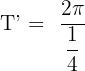
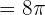
Hence, the period of the function 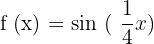 is
is  .
.
Example 6
Find the amplitude and frequency of the following function:
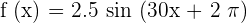
Solution
The amplitude of the function is straightforward . It is 2.5 in the above function.
Now, let us compute the frequency. To calculate the frequency of the periodic function, we need to calculate its period.
We know that the period of the above function is 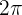 . So, the value of T is
. So, the value of T is 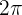 . Now, let us see what is the value of k. This function is given in the form
. Now, let us see what is the value of k. This function is given in the form  . Hence, the value of k is 30. We will substitute these values of T and k in the below formula to get the period of the function in this example:
. Hence, the value of k is 30. We will substitute these values of T and k in the below formula to get the period of the function in this example:
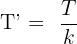
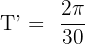
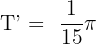
To find the frequency, we will take the reciprocal of the period:
Frequency = 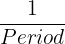
Frequency = 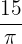
Example 7
Find the period of the following tangent function:
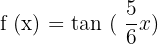
Solution
We know that the period of the tangent function 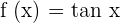 is
is  . So, the value of T is
. So, the value of T is  . Now, let us see what is the value of k. The function in this example is given in the form
. Now, let us see what is the value of k. The function in this example is given in the form 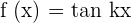 , where
, where 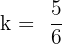 . We will substitute these values of T and k in the below formula to get the period of the function in this example:
. We will substitute these values of T and k in the below formula to get the period of the function in this example:
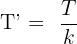
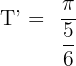

Hence, the period of the function 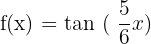 is
is 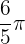
Summarise with AI:













I have math qstn problm
Break even point