In the world of sequence and series, one of the places of interest is the bounded sequence. Not all sequences are bonded. In this lecture, you will learn which sequences are bonded and how they are bonded?

Monotonic and Not Monotonic
To better understanding, we got two sequences for you. One is the 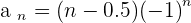 and other is the
and other is the 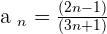 . Let's talk about
. Let's talk about 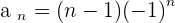 and construct the results for different values of n.
and construct the results for different values of n.
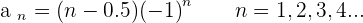
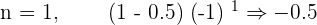
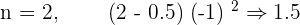

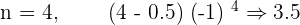
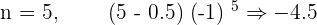
The sign changes alternatively. These types of series have no upper limit neither lower limit. This is because the amount which the series is growing on the positive end is equal to the amount that is decreasing on the negative end. We call them Not Monotonic. For the case of 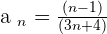 , let's construct the results.
, let's construct the results.
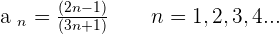
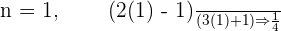
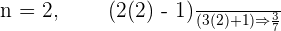


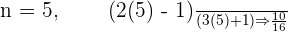
As you can note that the numerator is increasing by 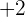 and denominator is increasing by
and denominator is increasing by  , hence we can conclude that the series is increasing. The positive end is increasing at some rate which mean that it has a bound. We call them Monotonic.
, hence we can conclude that the series is increasing. The positive end is increasing at some rate which mean that it has a bound. We call them Monotonic.
Bounded Sequence
Now you know that when we are talking about the bounded sequence, we are talking about the monotonic sequence. A bounded sequence can be either positive or negative, how you are going to find out? That is why mathematicians categorized the bounded sequence into two types. One of them is Bounded Below and other is the Bounded Above.
Bounded Below
A sequence is bounded below if all its terms are greater than or equal to a number, K, which is called the lower bound of the sequence.
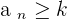
The greatest lower bound is called the infimum.
Bounded Above
A sequence is bounded above if all its terms are less than or equal to a number K', which is called the upper bound of the sequence.

The smallest upper bound is called the supremum.
Bounded Sequence
A sequence is bounded if it is bounded above and below, that is to say, if there is a number, k, less than or equal to all the terms of sequence and another number, K', greater than or equal to all the terms of the sequence. Therefore, all the terms in the sequence are between k and K'.

Examples
Study the following sequences and determine if they are bounded.
1 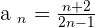
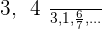
As the sequence is decreasing, 3 is an upper bound and the supremum.
To find the infimum or lower bound, we have two methods.
METHOD NO.1
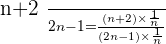

Since we want to find the lower bond and the sequence is decreasing, we will put the limits to infinity.

The limit is  .
.
 is a lower bound and the infimum.
is a lower bound and the infimum.
METHOD NO.2

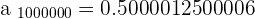
The limit is  .
.
 is a lower bound and the infimum.
is a lower bound and the infimum.
Thus, the sequence is bounded.

2 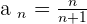

As the sequence is increasing,  is a lower bound and the infimum.
is a lower bound and the infimum.
METHOD NO.1
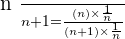

Since we want to find the lower bond and the sequence is decreasing, we will put the limits to infinity.

The limit is  .
.
 is a lower bound and the infimum.
is a lower bound and the infimum.
METHOD NO.2
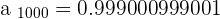
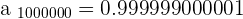
The limit is  .
.
 is an upper bound and the supremum.
is an upper bound and the supremum.
Thus, the sequence is bounded.
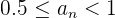













I have math qstn problm
Break even point