
Introduction
An arithmetic sequence is a list of numbers where each term increases or decreases by the same fixed amount, called the common difference.
For example:
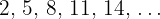
Here, the common difference is 3.
The nth term of an arithmetic sequence is given by:
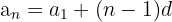
where 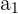 is the first term and d is the common difference.
is the first term and d is the common difference.
The sum of the first n terms is:
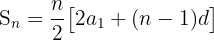
Example
The 3rd term of an arithmetic sequence is 10, and the 7th term is 22. Find the first term and the common difference.
Solution:
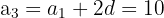
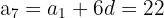
Subtracting the first from the second:
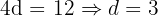
Substitute back:
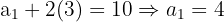
So the sequence is:
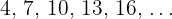
Practice Questions & Solutions
The fourth term of an arithmetic sequence is 14 and the sixth term is 20. Determine the sequence.
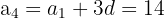
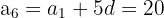
Subtract:
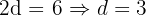
Then:
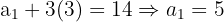
Sequence:
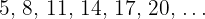
The first term of an arithmetic sequence is 3 and the fifteenth term is 45. Find the common difference and the sum of the first fifteen terms.
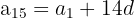
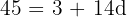
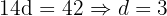
Sum of the first 15 terms:
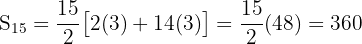
Common difference:
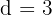
Sum:
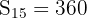
Find the sum of the first fifteen multiples of 7.
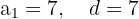
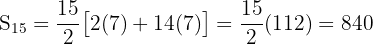
Sum:
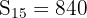
Find the sum of the first fifteen numbers ending in 5.

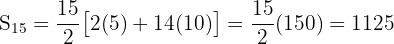
Sum:
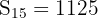
Find the sum of the first fifteen even numbers greater than 20.
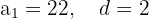
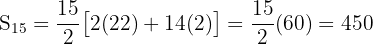
Sum:
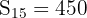
Find the angles of a convex quadrilateral, knowing they are in arithmetic sequence and their sum is 360 degrees.
Let the angles be:
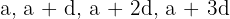
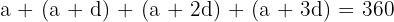
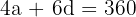
If 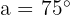 and
and 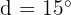 , then the angles are:
, then the angles are:
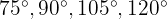
The shorter leg of a right triangle is 6cm. The sides form an arithmetic sequence. Find the lengths of the other two sides.
Let the sides be:
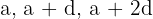
Given  :
:
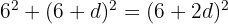
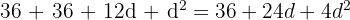
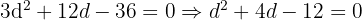
Solve for d:
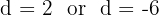
Reject the negative value.
Sides:
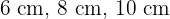
Find three numbers in an arithmetic sequence whose sum is 15 and the sum of their squares is 83.
Let the numbers be:
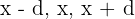
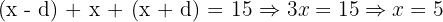
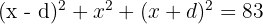
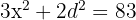
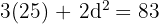
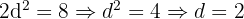
Numbers:
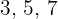












I have math qstn problm
Break even point