Chapters

What is a Limit?
Limits are one of the basic building blocks of calculus - however, it is sometimes hard to understand their properties. In order to explore the properties of limits, let’s define what a limit is.
When we talk about limits, we usually are dealing with functions. A limit is defined as some value that a function approaches when the input of that function reaches a specific value. Let’s break this down: a function takes a number as an input and gives a number as an output.
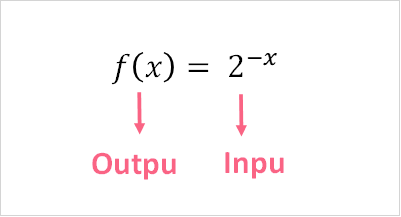
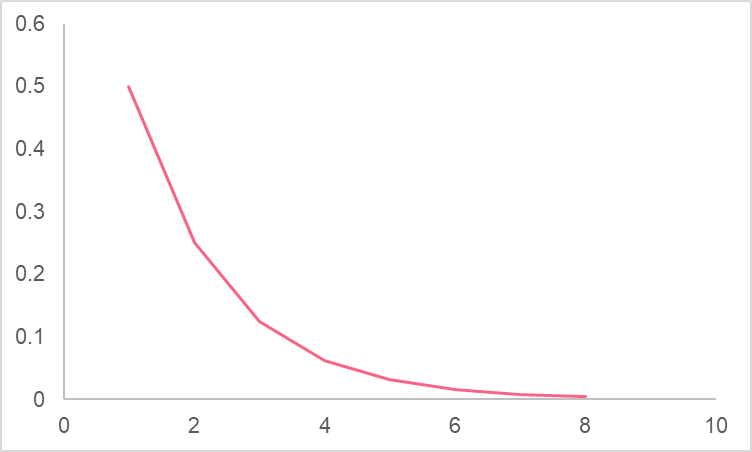
As you can see, when the input approaches higher and higher values, the output gets closer and closer to zero. This is an example of the limit of a function.
Approaching 1
When we talk about ‘approaching’ a value in math, we mean that we never actually get to that value. Let’s take the following function.

Let’s try to set x = 1.

This result is actually a special value known as the indeterminate form, which means that we don’t actually know the true value of them. Because the function at x = 1 is unknown, we can instead try approaching 1.
| x | y |
| 0.8 | 2.44000 |
| 0.9 | 2.71000 |
| 0.99 | 2.97010 |
| 0.999 | 2.99700 |
| 0.9999 | 2.99970 |
| 0.99999 | 2.99997 |
This is called approaching the limit from the ‘left,’ which is easier to understand by looking at a number line.

We can see that when x approaches 1, it gets close to 3, which is the limit.
Approaching Infinity
One common task you will see when working with limits is being asked to approach infinity. Infinity, however, is defined as an endless number. How can we approach, or calculate, something that is endless?
| 10 |
| 10,000 |
| 1,000,000 |
| ... |
 |
We can apply the same method we used in the previous example. Take a look at this common function:

If we set x = infinity, we would get another undefined, or unknown, value. However, we can approach infinity by plugging in bigger and bigger values.
| x | y |
| 10 | 0.1 |
| 100 | 0.01 |
| 1000 | 0.001 |
| 10000 | 0.0001 |
| 100000 | 0.00001 |
| 1000000 | 0.000001 |
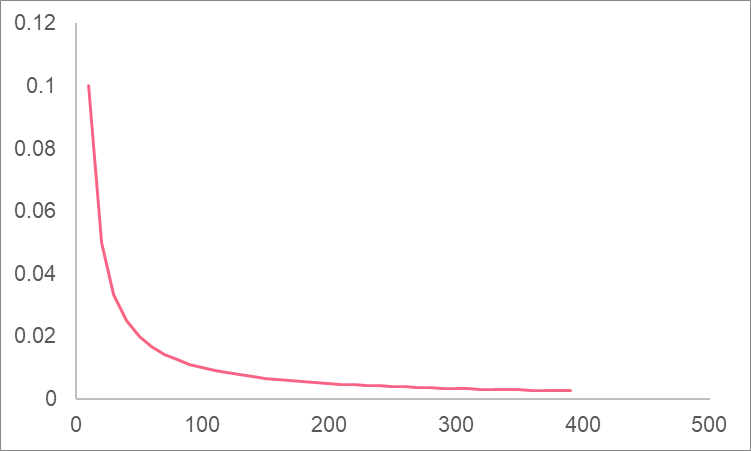
When we graph this, we can see that as x approaches infinity, the output approaches zero. This is the limit of this function.
Limit Notation
So far we have talked about the definition of a limit and some examples. Now, let’s turn to the formal, mathematical notation of limits. You will typically see limit notation like this:

| a | Value that we’re approaching |
| f(x) | Function |
| c | The limit |
| lim | Limit symbol |
Recall that we talked about approaching a limit from the ‘left’ or ‘right’ side. This distinction is written as the following.

| +a | Approach from the right |
| -a | Approach from the left |
Verbally, we say that as x approaches a, then the function f(x) approaches the value c. Let’s take the example in the previous section, where we worked with infinity.

Here, we would say that as x approaches infinity, the function 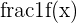 approaches 0.
approaches 0.
Limits of a Function
There are several different ways you can find the limit of a function. The easiest and most natural method is to simply substitute the value a as the input. Let’s take an example.
Previously, when we substituted infinity into the function 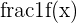 , we had an undefined value. Here, we can substitute 10 into the function without any issues because it is defined.
, we had an undefined value. Here, we can substitute 10 into the function without any issues because it is defined.

When we have an undefined value or indeterminate form, what should we do? There are a couple of different ways you can do this, described in the table below.
| Method | When to Use | |
| Method 2 | Simplify the function | When plugging in the value a results in an indeterminate form |
| Method 3 | L’Hopital’s Rule | Indeterminate forms like  or or 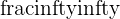 |
Continuity
Continuity is an important concept when it comes to functions and limits. A function is continuous if there are no breaks of any kind on the graph. Let’s take a look at some examples of non-continuous functions.
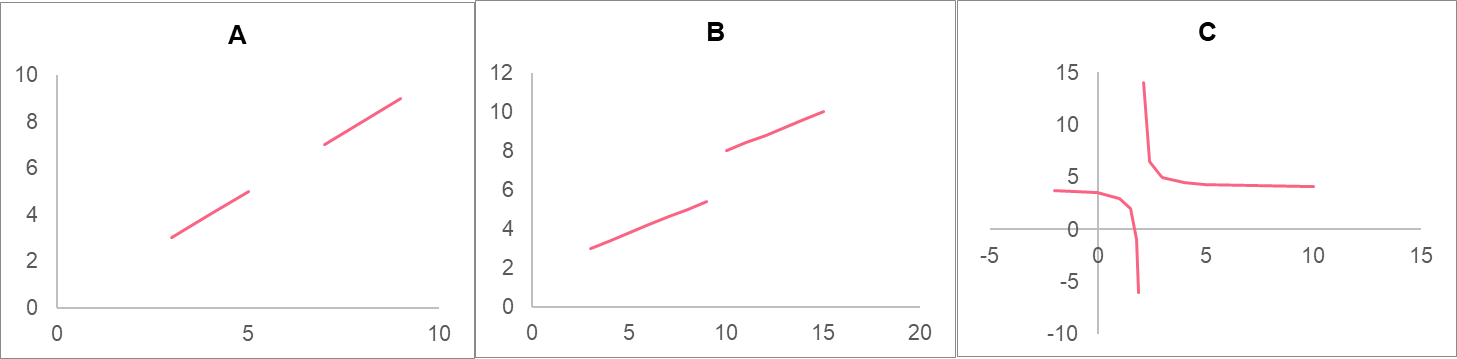
| A | B | C |
| Vertical asymptote | Break | Jump |
Break
When there are breaks in the graph of any kind, many important rules and methods can’t be applied to a function at that point. Let’s take a look at the formal definition of continuity.

| A | B |
| If f(c) exists | If the limit at x=c exists |
Properties of Limits
In order to find the limit of a function, there are several rules you can use in order to make finding the limit easier.
Sum Rule
The sum rule states that the limit as x approaches a value a of the sum of two functions, f(x) + g(x), is the same thing as the limit as x approaches value a of f(x) plus the limit as x approaches value a of g(x).
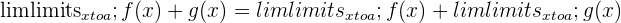 | The limit of the sum of two functions = The sum of their limits |
Constant Rule
The constant rule involves constant functions. A constant function is any function that is one constant c.
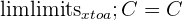 | The limit of a constant function = constant |
Product Rule
The product rule states as x approaches a value a of the product of two functions, f(x) * g(x), is the same thing as the limit as x approaches value a of f(x) multiplied by the limit as x approaches value a of g(x).
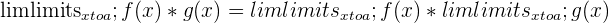 | The limit of the product of two functions = The product of their limits |













I have math qstn problm
Break even point