Chapters

What are Composite Functions?
In order to understand what a composite function is, let’s take a look at the most basic function.

This is a linear function. The table below defines the elements inside of a linear function.

| A | - | y | output |
| B | 3 | m | slope |
| C | - | x | input |
| D | 1 | b | y-intercept |
A function takes numbers as inputs, performs a transformation on them, and results a number as output. Let’s plug in some numbers as inputs to our linear function to test it out.
| x | y |
| -3 | -8 |
| -2 | -5 |
| -1 | -2 |
| 0 | 1 |
| 1 | 4 |
| 2 | 7 |
| 3 | 10 |
Now, let’s look at a composite function. A composite function is applying one function to another. That is, we get the output of one function and plug it into another function.
| Step 1 | Plug in a number to f(x) |
| Step 2 | Get the result of f(x) |
| Step 3 | Plug the result into g(x) |
Let’s take a look at an example using our linear function above. Take the following two functions.
| Function 1 | f(x) = 3x + 1 |
| Function 2 | g(x) = 5x |
As an example, let’s solve g(f(x)) with the input 2.
| 1 | f(2) = 3(2) + 1 = 7 |
| 2 | g(7) = 5(7) |
| 3 | = 35 |
While this was pretty easy, solving composite functions can get more complex with more complex functions. This is why, instead of the three steps we performed above, we can just simplify the formula first.
| 1 | g(f(x) = 5(f(x)) |
| 2 | 5(f(x)) = 5(3x+1) |
| 3 | = 15x + 5 |
Plugging in the number 2, we can see that we get the same result:
\[
15(2) + 5 = 30 + 5 = 35
\]
The notation for composite functions is written in the table below.
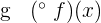 | Take the result of f(x) | f(x) = 3x g(x) = x + 5 g(f(2)) = 3(2) + 5 = 11 |
 | The same as above | f(x) = x + 2 g(x) = 4x g(f(1)) = 4(1 + 2) = 12 |
Common Composite Functions
Now that you’ve been exposed to more functions, let’s go through a few common forms that composite functions can take on using three functions as an example.
| f(x) | g(x) | h(x) |
 |  | 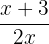 |
| Addition | Division | Addition, division, multiplication |
The first example is:
\[
g \; (^{\circ} \; f)(x)
\]
The process to solve this composite function is in the table below.
| f(x) | g(f(2)) | |
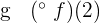 | 2 + 3 = 5 | g(5) =  = 0.2 = 0.2 |
The second example is:
\[
f \; (^{\circ} \; g)(x)
\]
The process to solve this composite function is in the table below.
| g(x) | f(g(2)) | |
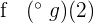 |  | f( ) = ) = 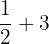 = 3.2 = 3.2 |
The third example is:
\[
f \; (^{\circ} \; g \; (^{\circ} \; h)(x)
\]
The process to solve this composite function is in the table below.
| f(x) | g(f(1)) | h(g(f(-2))) | |
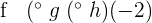 | -2+3 = 1 | g(1) =  = 1 = 1 | h(1) = 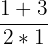 = 2 = 2 |
The last example is:
\[
f^{-1}(x)
\]
The process to solve this composite function is in the table below.
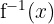 | Inverse | Process | Comparison |
| This is the inverse of a function, which means we need to take the inverse | f(x) = x + 3 y = x + 3 y - 3 = x
| To get the inverse, we simply need to get x on one side. | f(2) = 2 + 3 = 5
|
Problem 1
Now that you know more about composite functions, write your own function for f(x). Next, calculate the composite function using g(x) that is given:
\[
g(x) = \frac{3x+1}{x}
\]
Plug in a few numbers and see what you come up with.
Problem 2
Solve the following function for the following values for x, making sure to show your work.
\[
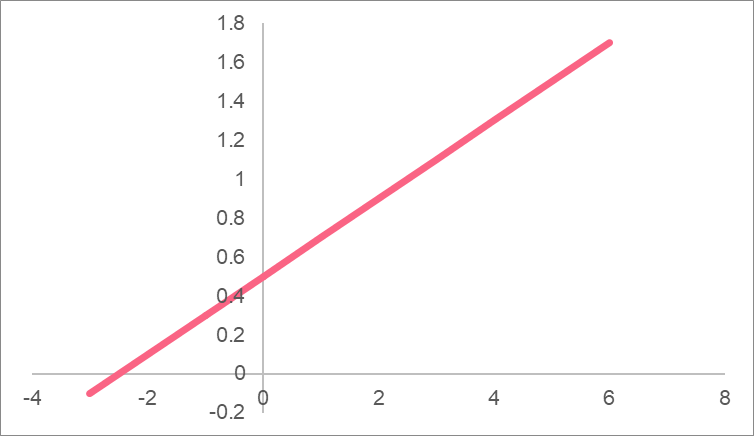
f(x) = \dfrac{2x+5}{10}
\]
Values for x:
- 4
- 1
- 2
Problem 3
You are given the following functions:
| f(x) | g(x) | |
| Function | x + 2 | x |
Simplify the composite function:
\[
\frac{f(x)}{g(x)}
\]
Problem 4
You are given the following functions:
| f(x) | g(x) | h(x) | |
| Function |  | 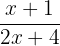 | 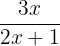 |
Solve the composite function:
\[
f \; (^{\circ} \; g \; (^{\circ} \; h)(3)
\]
Problem 5
You have the following function:
\[
f(x) = \frac{x^{2} + 4x + 4}{x+2}
\]
Calculate the inverse of this function.
Solution Problem 1
You were asked to come up with your own function. Then, calculate g(f(x)) for a couple of values.
\[
g(x) = \frac{3x+1}{x}
\]
Let’s take the following function as an example:
\[
f(x) = x + 2
\]
Here are some sample values.
| f(x) | g(f(x)) | |
| 1 | f(1) = 1 + 2 = 3 | g(3) = 4 |
| 4 | f(3) = 3 + 2 = 5 | g(5) = 3.25 |
| 10 | f(6) = 6 + 2 = 8 | g(8) = 3.1 |
Solution Problem 2
You were asked to show the following values of x for the following function:
\[
f(x) = \dfrac{2x+5}{10}
\]
Values for x:
- f(4) =
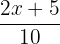 = 1.3
= 1.3 - f(1) =
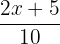 = 0.7
= 0.7 - f(2) =
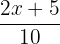 = 0.9
= 0.9
Here is the plot for this function:
Solution Problem 3
You needed to simplify the composite function for these two functions:
| f(x) | g(x) | |
| Function | x + 2 | x |
\[
\frac{f(x)}{g(x)} = \frac{x+2}{x}
\]
\[
\frac{f(x)}{g(x)} = \frac{x}{x} + \frac{2}{x}
\]
\[
\frac{f(x)}{g(x)} = 1 + \frac{2}{x}
\]
Solution Problem 4
You had to solve the composite function given these three functions:
| f(x) | g(x) | h(x) | |
| Function |  | 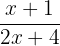 | 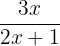 |
Solve the composite function:
\[
f \; (^{\circ} \; g \; (^{\circ} \; h)(3) = f(g(h(3)))
\]
\[
h(3) = \frac{3*3}{2*3+1} = \frac{9}{7} = 1.29
\]
\[
g(1.29) = \frac{1.29+1}{2(1.29)+4} = 0.35
\]
\[
f(0.35) = 0.35^{2} = 0.12
\]

Solution Problem 5
Let’s take the inverse of the following function:
\[
f(x) = \frac{x^{2} + 4x + 4}{x+2}
\]
\[
f(x) = \frac{(x+2)^{2}}{x+2}
\]
\[
f(x) = \frac{(x+2)(x+2)}{x+2}
\]
\[
f(x) = (x+2)
\]
\[
y = x+2
\]
\[
y -2 = x
\]
\[
f^{-1}(x) = y - 2
\]










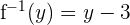
 = 5 - 3 = 2
= 5 - 3 = 2


I have math qstn problm
Break even point