Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10
- Solution of exercise 11

The best Maths tutors available
Exercise 1
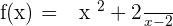
Exercise 2
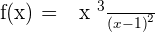
Exercise 3

Exercise 4
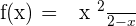
Exercise 5
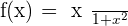
Exercise 6
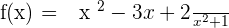
Exercise 7

Exercise 8
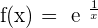
Exercise 9

Exercise 10
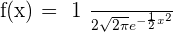
Exercise 11
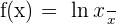
Solution of exercise 1
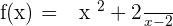
Horizontal asymptotes
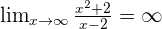

Vertical asymptotes.
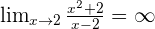
Oblique asymptotes.
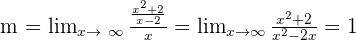
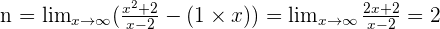
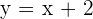
Solution of exercise 2
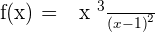
Horizontal asymptotes

Vertical asymptotes.
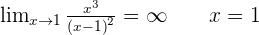
Oblique asymptotes.
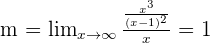

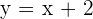
Solution of exercise 3

Horizontal asymptotes
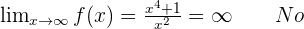
Vertical asymptotes.
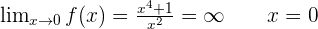
Oblique asymptotes.
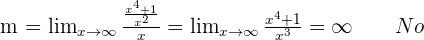
Solution of exercise 4
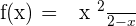
Horizontal asymptotes
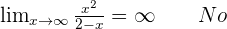
Vertical asymptotes.

Oblique asymptotes.
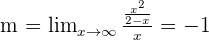
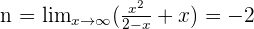

Solution of exercise 5
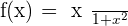
Horizontal asymptotes

No vertical or oblique asymptote.
Solution of exercise 6
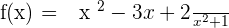
Horizontal asymptotes

No vertical or oblique asymptote.
Solution of exercise 7


Horizontal asymptotes.

No Horizontal Asymptote.
Vertical asymptotes.
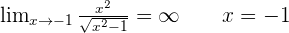
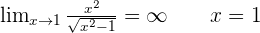
Oblique asymptotes.
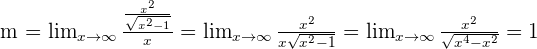
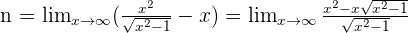
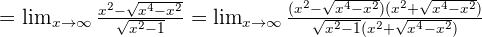


Solution of exercise 8
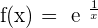
Horizontal asymptotes
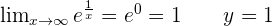
Vertical asymptotes.
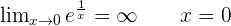
Solution of exercise 9

Horizontal asymptotes
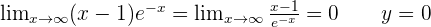
No vertical or oblique asymptote.
Solution of exercise 10
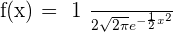
Horizontal asymptotes
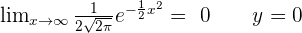
No vertical or oblique asymptote.
Solution of exercise 11
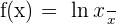
Horizontal asymptotes
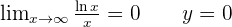
Vertical asymptotes.













I have math qstn problm
Break even point