Chapters

What is Linear Function?
A linear function is one of the fundamentals for solving complex mathematical equations. As the word, "Linear", tells you that we will be talking about straight lines in this lesson. A linear function is an equation of a straight line. The slope of the line could vary, however, the line will remain straight till infinity. Linear equations are easy to understand because it doesn't require any other complex understanding, unlike other equations. The easiest way to spot a linear function is by looking at the equation. If the equation's variable has a degree of "1" that means you are working with a linear equation.
Syntax, Graph, and Understanding of Linear Equation
The equation of a linear function is:

y = mx + b
Its graph is an oblique straight line, which is defined by two points of the function. For example, we have a linear equation, 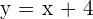 . To draw this line, we need two points. The easiest way to find two points for a linear equation is to put one component equal to zero to find another component like this,
. To draw this line, we need two points. The easiest way to find two points for a linear equation is to put one component equal to zero to find another component like this, 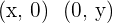 , and then find the unknown points.
, and then find the unknown points.
 |  |  |
|---|---|---|
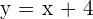 |  |  |
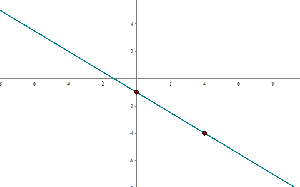
Once you found two points, mark it on the graph and then connect both points by drawing a straight line passing through both points. It will be like this
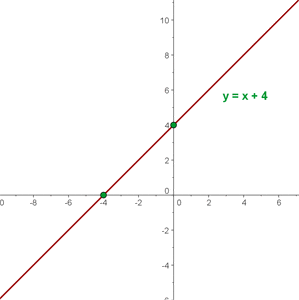
Let's take a close look at the equation,  .
.
We all know what is y and x mean here, they are the coordinates of the graph but the real question is what is m and c?
The "m" is the slope of the straight line.
The slope is the inclination of the line with respect to the x-axis.
If 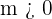 , the function is increasing and the angle of the line with the positive x-axis is acute.
, the function is increasing and the angle of the line with the positive x-axis is acute.

If  , the function is decreasing and the angle between the line with the positive x-axis is obtuse.
, the function is decreasing and the angle between the line with the positive x-axis is obtuse.
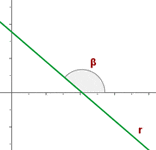
The formula to find gradient/slope of a line is 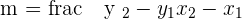 .
.
Two parallel lines have the same slope.

 is the y-intercept and indicates the intersecting point of the line with the vertical axis.
is the y-intercept and indicates the intersecting point of the line with the vertical axis.

If 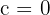 , the equation of a linear function is:
, the equation of a linear function is:
y = mx
It means that the graph of the linear function is a straight line passing through the origin.

 |  |  |  |  |  |
|---|---|---|---|---|---|
 |  |  |  |  |  |

Identity Function
The identity function is a type of function that will return the same value which was used as its input or argument.

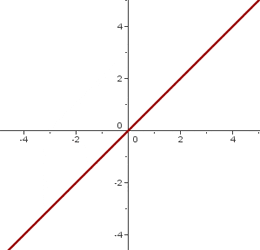
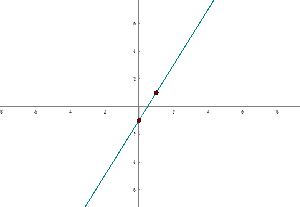
Examples of Linear Function
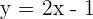
 |  |
|---|---|
 |  |
 |  |
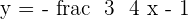
 | 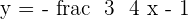 |
|---|---|
 |  |
 |  |












I have math qstn problm
Break even point