Polynomial Function
To understand the meaning of a rational function, you should first understand what a polynomial is. A polynomial function is a function made up of monomials that have variables. The following are examples of monomials.
If we break down each monomial, we can see clearly that they are made up of the following.
| A | Constant |
| B | Variable |
| C, D | Constant and 1 or more variables |
A polynomial is made up of monomials. Take a look at some of the examples below.
These four polynomials can be classified based on the number of monomials they contain.
| A | Monomial | One monomial |
| B | Binomial | Two monomials |
| C | Trinomial | Three monomials |
| D | Polynomial | 4 or more monomials |
Rational Function Definition
A rational function is any polynomial function divided by another polynomial function. The reason behind the name ‘rational function’ is the term ‘ratio,’ which is simply a fraction.
The image above is an example of a ratio, which can be written in fraction form. In practice, any polynomial can be a rational function, the reason why is explained in the image below.
As you can see, any polynomial can be divided by the monomial 1. Here are some more examples of rational functions.
| Numerator | Denominator | |
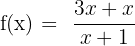 | Binomial | Binomial |
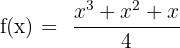 | Trinomial | Monomial |
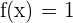 | Constant | Constant |
Linear Function
A linear function is a special type of polynomial. As the name implies, a linear function is any function that involves a linear equation. A linear equation is any equation that results in a linear relationship.
| y | Output |
| m | Slope |
| x | Input |
| b | Y-intercept |
Some examples of linear equations can be seen below.
| A |  |
| B |  |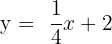
| C |  |
Rational Function Rules
There are many useful rules that you should know for rational functions. Let’s take a look at the rules for linear functions first. Here are the rules you should follow in order to find the slope, y-intercept and any point on a line.
| Slope from two points |  |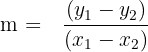
| Y-intercept | b = mx = y |
| Point on a line | Plug in any x to get a point (x,y) |
In terms of polynomials, we have several special polynomials that you should be familiar with.
| Quadratic |  |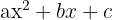
| Cubic |  |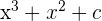
| Circle |  |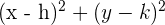
| Ellipse |  |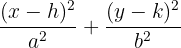
One of the most important things you will do when working with rational functions is simplify the polynomials that make them up. A rational function can be written as follows. 
Problem 1
Classify the following functions as either rational or non-rational functions. Justify why you think each function is either rational or non-rational. If they are rational, say what kind of polynomials they are.
| 1 | f(x) =  |
| 2 | f(x) = |
| 3 | f(x) = |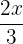
| 4 | f(x) = |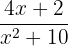
Problem 2
You are given the following polynomial. First, simplify this polynomial. Next, state what kind of polynomial it is and graph it.
\[ f(x) = 2(\sqrt{x^{2}} + 2) \]
Problem 3
Simplify the following polynomial, making sure to include all the steps you took to simplify this polynomial.
\[ f(x) = (2x + 5)^{2} \]
Problem 4
Simplify the following polynomial, making sure to include all the steps you took to simplify this polynomial.
\[ f(x) = 8x^{3} -27 \]
Problem 5
Simplify the following rational function, making sure to include all the steps you took to simplify this polynomial.
\[ f(x) = \frac{(x + 3)^{2}}{(2x-4)(4x^{2} + 8x + 16)} \]
Solution Problem 1
In this problem, you were asked to classify the following functions as either rational or non-rational functions. You were also tasked with saying what kind of polynomials they are. The answer to this problem can be found below.
| 1 | f(x) = | Non-rational: includes an imaginary number | N/A |
| 2 | f(x) = | Rational: constant | Monomial |
| 3 | f(x) = 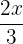| Rational: two polynomials | Two monomials |
| 4 | f(x) = 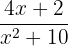| Rational: two polynomials | Two binomials |
Solution Problem 2
In this problem you were given the following polynomial. After simplifying this polynomial, you were asked to graph it. The first step we should take is to simplify the x term. Notice that it is the square root of a square, which always gives us the number itself.
\[ f(x) = 2(\sqrt{x^{2}} + 2) \]
\[ f(x) = 2(x + 2) \] Now, we just distribute the 2 across the binomial.
\[ f(x) = 2x + 4 \]
This is clearly a linear equation. Plotting this linear equation, we get the following:
| x | y |
| -2 | 0 |
| -1 | 2 |
| 0 | 4 |
| 1 | 6 |
| 2 | 8 |
| 3 | 10 |
In this problem you were asked to simplify the following polynomial. \[ f(x) = (2x + 5)^{2} \] First, we want to write the formula. \[ f(x) = (2x + 5)(2x + 5) \] Next, we multiply each of the terms with each other. \[ f(x) = 4x^{2} + 25 + 10x + 10 x = 4x^{2} + 20x + 25 \] Or, we can simply use the rule: \[ f(x) = (2^{2})x^{2} + 2(2x*5) + 5^{2} \] Here is how you simplify the following polynomial. \[ f(x) = (2x - 3)(4x^{2} + 6x + 9) \] First, you should be able to recognize this type of pattern. Because we’re multiplying a binomial and a trinomial, we should always check if we can use a rule. Luckily, we can use the rule from before, as we’re dealing with multiples of 3. \[ f(x) = (2x - 3)(4x^{2} + 6x + 9) = 8x^{3} - 27 \] For this rational function, we can combine what we’ve learned to simplify the numerator and denominator. \[ f(x) = \frac{(x + 3)^{2}}{(2x-4)(4x^{2} + 8x + 16)} \] \[ \frac{(x+3)(x+3)}{(2x-4)(4x^{2} + 8x + 16)} \] 
Solution Problem 3
Solution Problem 4
Solution Problem 5
Summarise with AI:
Did you like this article? Rate it!
Loading...
I get it somehow, there are others who are unfamiliar and I have a hard time with it but it’s okay that I get it.
Thanks for sharing your thoughts! It’s completely normal to find some parts unfamiliar or more difficult than others. The important thing is that you’re making progress and understanding more as you practise. Keep going! 😊
At least I understood some of it, but there are others that I’m confused about and have a hard time understanding, but I get it.
Thanks for sharing! It’s great that you’ve understood some of it already. Don’t worry if a few parts are still confusing — keep practising and take your time with the trickier sections. You’ll get there! 😊
The lesson was a little difficult for me, especially the word problems, but the examples helped me understand it better.
Thanks for your feedback! Word problems can definitely be tricky, so we’re glad the examples helped make the lesson clearer. Keep practising — it gets easier with time! 😊
Thankyouuu po