Chapters

Series and Sequence
One of the basic concepts in mathematics is sequences and series. A sequence depicts the collection of items in which any kind of repetition is allowed. On the other hand, the series represents the sum of all elements in the sequence. We can define sequence as:
"A list of numbers arranged in a sequential order. There is a particular relationship between all terms in the sequence"
A series can be defined as:
"The sum of all the terms in the sequence is known as series"
These series and sequences can be better comprehended by understanding the relevant formulas. Although sequences resemble sets, however, the main difference between the sets and sequences is that in a sequence, the numbers can occur repeatedly.
Types of Sequences
In this article, we have compiled a list of all the formulae related to the series and sequences. We will specifically discuss the following sequences and their formulas:
- Arithmetic sequence
- Geometric sequence
- Fibonacci sequence
- Harmonic sequence
Arithmetic Sequence
When a series of numbers are arranged in a specific pattern, we call it a sequence. An arithmetic sequence means the numbers arranged in such a way that the difference between two consecutive terms is the same. Arithmetic progression is another name given to the arithmetic sequence. This difference is termed as common difference and is represented by d. This common difference also helps to determine the next term in the sequence. All you have to do is to add the common difference in the term to get the next term. We can have an increasing or decreasing arithmetic sequence.
- If an arithmetic sequence is increasing, the common difference is positive
- If an arithmetic sequence is decreasing, then the common difference is negative
Consider the following example:
14, 17, 20, 23, 26, 29, 32
You can see in the above example that each next term is obtained by adding a fixed number 3 to the previous term. This constant 3 is known as common difference (d). Since this constant is positive, so we can say that the arithmetic sequence is increasing.
Consider another example below:
50, 46, 42, 38, ....
In the above sequence, the difference between the successor and predecessor is -4. Hence, the sequence is decreasing.
Now, let us see what are some of the formulae related to the arithmetic sequence.
Formula for Finding the Sum of the Arithmetic Sequence
Use the following formula to compute the sum of arithmetic sequence:
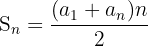
Here,
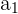 = First term of the sequence
= First term of the sequence
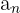 = The nth term of the sequence
= The nth term of the sequence
 = The number of terms in the series
= The number of terms in the series
Geometric Sequence
In a geometric sequence, each term is obtained by multiplying or dividing the previous term with a particular number. The number which is multiplied or divided by the previous term to get the next term is known as a common ratio and is denoted by r. A geometric sequence is also known as geometric progression. Consider the following example:
4, 8, 16, 32, 64,...
You can see that in the above example, each successive term is obtained by multiplying the previous term by a fixed constant 2. This constant is also known as common ratio.
Consider another example below:
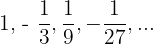
In the above example, each next term is found by multiplying the previous term by a fixed term 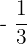 . This shows that the common ration can be negative or positive.
. This shows that the common ration can be negative or positive.
Formula for Finding the Sum of the Geometric Sequence
Use the following formula to compute the sum of geometric sequence:
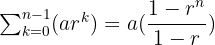
Here:
 = First term of the sequence
= First term of the sequence = common ratio
= common ratio = The number at which the nth term of the sequence is located
= The number at which the nth term of the sequence is locatedFibonacci Sequence
Fibonacci sequences are one of the interesting sequences in which every next term is obtained by adding two previous terms. This sequence starts with the digits 0 and 1. Consider the following example:
0, 1, 1, 2, 3, 5, 8, 13, ....
You can see that each next term is an aggregate to the previous two terms. For instance, 2 is obtained by adding the last two terms 1 + 1. Similarly, 13 is obtained by adding 5 and 8 together. This sequence is defined recursively which means that the previous terms define the next terms.
Formula for Finding the Nth Term in the Fibonacci Sequence
As discussed earlier, the first two terms of the Fibonacci sequence are always 0 and 1. Hence, we can denote these terms in the Fibonacci sequence like this:

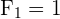
The formula for computing the nth term in the Fibonacci sequence is given below:
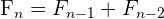
Harmonic Sequence
When we take reciprocal of each term in the arithmetic sequence, a new sequence is formed which is known as a harmonic sequence. The general notation of a harmonic sequence is given below:
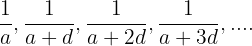
Here, a cannot be zero.
Harmonic sequence is also called harmonic progression. Consider the following example:
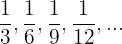
In the above example, the reciprocal of the terms would give us the following arithmetic sequence, therefore we can say that the list is arranged in a harmonic sequence.
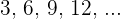
The difference between the consecutive terms is a constant 3, therefore the sequence is an arithmetic sequence.
Formula for Finding the Nth Term of an Arithmetic Sequence
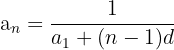
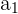 = First term of the sequence
= First term of the sequenceFormula for Finding the Sum of the Harmonic Sequence
The sum of the harmonic sequence is known as harmonic series. The formula for computing the sum of series is given below:
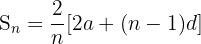










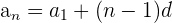
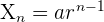
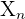 = nth term of the sequence
= nth term of the sequence


I have math qstn problm
Break even point