Chapters
- Find the Intervals of Concavity and Convexity for the Following Functions:
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10
- Solution of exercise 11
- Solution of exercise 12

The best Maths tutors available
Find the Intervals of Concavity and Convexity for the Following Functions:
Exercise 1
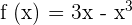
Exercise 2
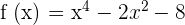
Exercise 3
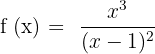
Exercise 4
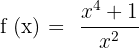
Exercise 5
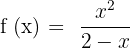
Exercise 6
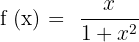
Exercise 7
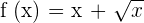
Exercise 8

Exercise 9
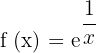
Exercise 10
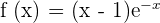
Exercise 11
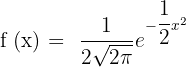
Exercise 12
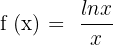
Solution of exercise 1
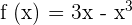
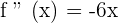
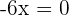

Convex: 
Concave: 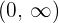
Solution of exercise 2
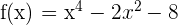

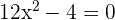
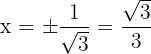
Concave: 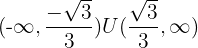
Convex: 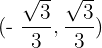
Solution of exercise 3
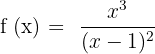
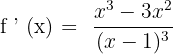
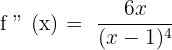
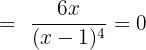

Convex: 
Concave: 
Solution of exercise 4
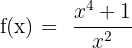
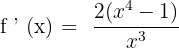
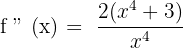
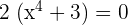

Convex: 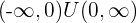
Solution of exercise 5
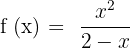
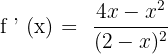
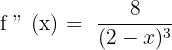
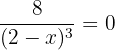
No solution
Convex: 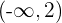
Concave: 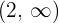
Solution of exercise 6
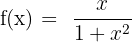
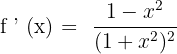
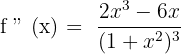
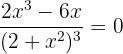

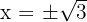
Convex: 
Concave: 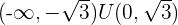
Solution of exercise 7
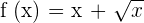
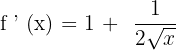
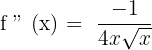
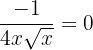
No solution
Concave: 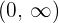
Solution of exercise 8



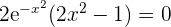
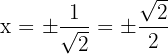
Inflection points: 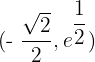 ,
, 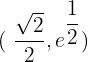
Convex: 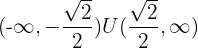
Concave: 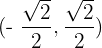
Solution of exercise 9
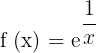
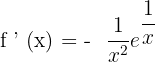
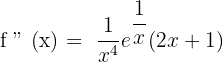
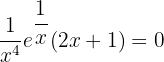
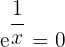 No solution
No solution

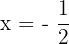
Convex: 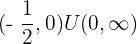
Concave: 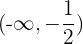
Solution of exercise 10
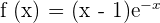
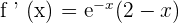
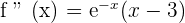


Convex: 
Concave: 
Solution of exercise 11
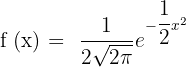
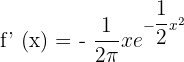
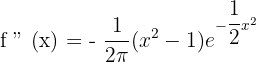
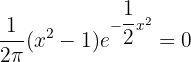
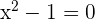

Convex: 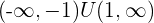
Concave: 
Solution of exercise 12
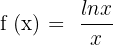
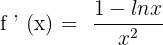
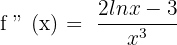
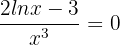
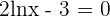
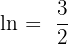
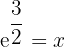
Convex: 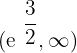
Concave: 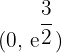
Summarise with AI:













Nice to see what you have provided.IT helps me a lo in my engineering mathematics.
i love it mwaaaaa :*