Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Exercise 13
- Exercise 14
- Exercise 15
- Exercise 16
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10
- Solution of exercise 11
- Solution of exercise 12
- Solution of exercise 13
- Solution of exercise 14
- Solution of exercise 15
- Solution of exercise 16

The best Maths tutors available
Exercise 1

Exercise 2
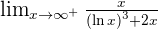
Exercise 3
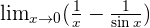
Exercise 4

Exercise 5
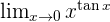
Exercise 6
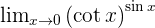
Exercise 7
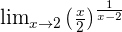
Exercise 8

Exercise 9
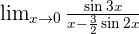
Exercise 10
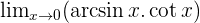
Exercise 11
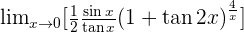
Exercise 12
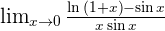
Exercise 13

Exercise 14
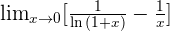
Exercise 15
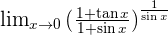
Exercise 16
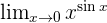
Solution of exercise 1


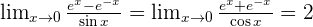
Solution of exercise 2
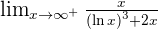
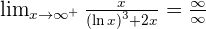
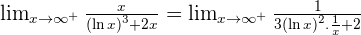
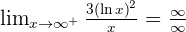

Solution of exercise 3
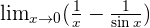
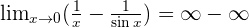
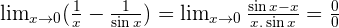
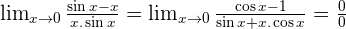
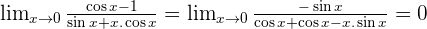
Solution of exercise 4

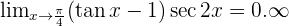

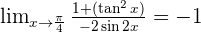
Solution of exercise 5
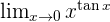
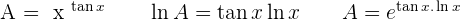

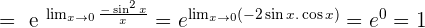
Solution of exercise 6
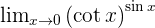



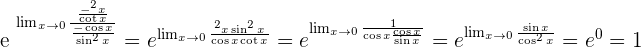
Solution of exercise 7
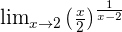
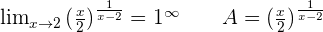
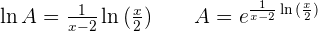

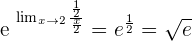
Solution of exercise 8

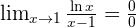
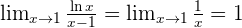
Solution of exercise 9
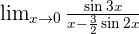
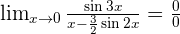
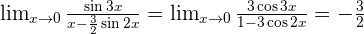
Solution of exercise 10
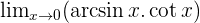
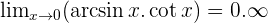
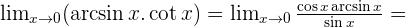
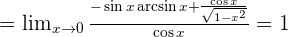
Solution of exercise 11
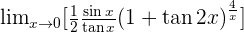
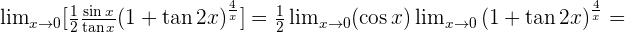


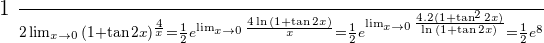
Solution of exercise 12
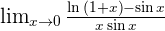

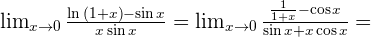

Solution of exercise 13

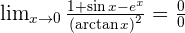
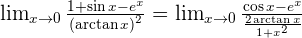
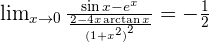
Solution of exercise 14
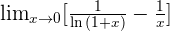

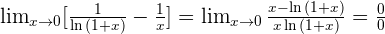
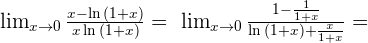

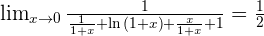
Solution of exercise 15
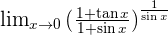
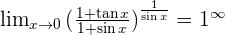

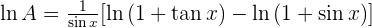



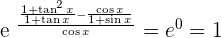
Solution of exercise 16
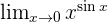

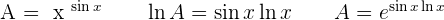

Summarise with AI:













Nice to see what you have provided.IT helps me a lo in my engineering mathematics.
i love it mwaaaaa :*