Chapters

Exercise 1
Calculate the intervals of increase and decrease of the following functions:
1. 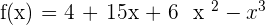
2. 
3. 
4. 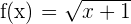
5. 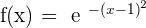
6. 
Exercise 2
Calculate the maximum and minimum values of the following functions:
1.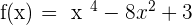
2.
3.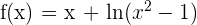
4.
Exercise 3
Find the intervals of concavity and convexity and the points of inflection for the following functions:
1.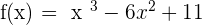
2.
3.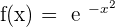
Exercise 4
The value of a stock on a particular day can be derived by the following formula: (Supposing that the stock exchange works every day of one month for 30 days.)

1. Determine the maximum and minimal values, as well as the days in which they happened.
2. Determine the time periods in which stocks rose or fell.
Exercise 5
Suppose that the yield, r, in the % of students in a one-hour exam is given by:
 .
.
Where 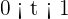 is the time in hours.
is the time in hours.
1. At what moments does the yield increase or decrease?
2. At what moments is the yield zero?
3. When is the biggest yield obtained and which is?
Solution of exercise 1
Calculate the intervals of increase and decrease of the following functions:
1. 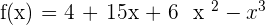
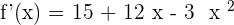
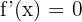
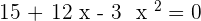
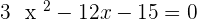
After solving the above equation:


Increasing: 
Decreasing: 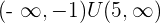
2. 

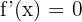
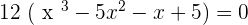

After solving the above equation:

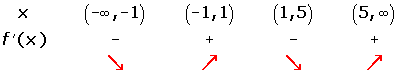
Increasing: 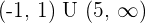
Decreasing: 
3. 
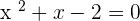
After solving the above equation:


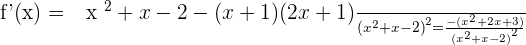
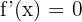

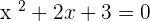
No solutions in  .
.
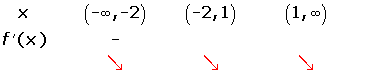
Decreasing: 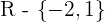
4. 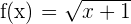

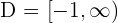

Increasing: 
5. 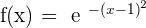
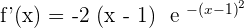
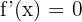
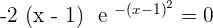

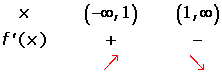
Increasing: 
Decreasing: 
6. 
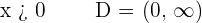

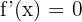

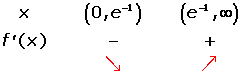
Increasing: 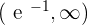
Decreasing: 
Solution of exercise 2
Calculate the maximum and minimum values of the following functions:
1.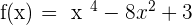

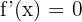


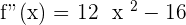
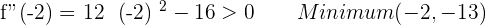


2.
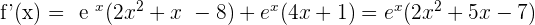
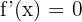
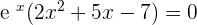

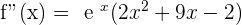

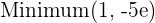


3.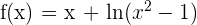
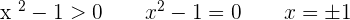

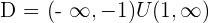

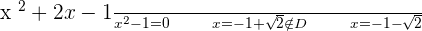
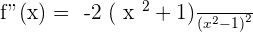
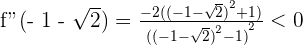
At  , there is a maximum
, there is a maximum
4.
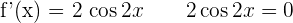

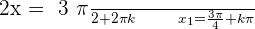
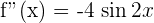
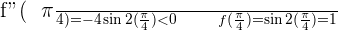

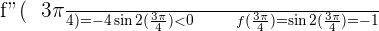

Solution of exercise 3
Find the intervals of concavity and convexity, and the points of inflection for the following the functions:
1.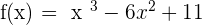



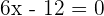


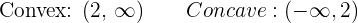
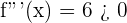
Inflection point 
2.

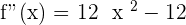

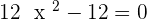


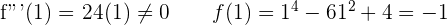

Inflection points: 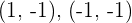
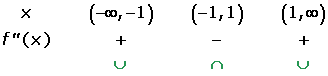

3.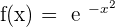


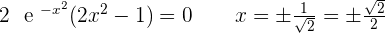
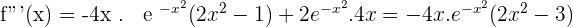
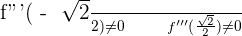
Inflection points: 

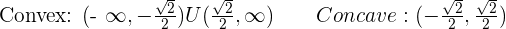
Solution of exercise 4
The value of a stock on a particular day can be derived by the following formula: (Supposing that the stock exchange works every day of one month for 30 days.)

1. Determine the maximum and minimal values, as well as the days in which they happened.
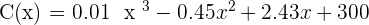


After solving the equation, we will get:

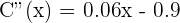
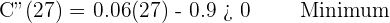

2. Determine the time periods in which stocks rose or fell.
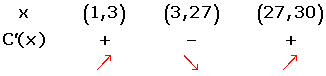
From days 1 to 3, and 27 to 30 the value of the stocks rose, and from days 3 to 27 the value of the stocks fell.
Solution of exercise 5
Suppose that the yield, r, in the % of students in a one-hour exam is given by:
 .
.
Where 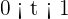 is the time in hours.
is the time in hours.
1. At what moments does the yield increase or decrease?


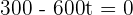
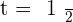
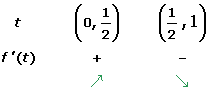
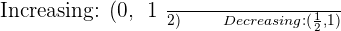
2. At what moments is the yield zero?

After solving the equation, we will get:

The yield is zero at the beginning 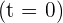 and at the end of the test
and at the end of the test  .
.
3. When is the biggest yield obtained and which is?
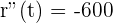
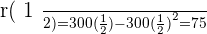
Maximum yield: 













I have math qstn problm
Break even point