Chapters

Exercise 1
Determine the domain of the following polynomial functions:
1 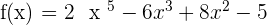
2 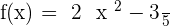
Exercise 2
Determine the domain of the following rational functions:
1 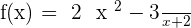
2 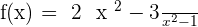
3 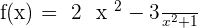
4 
5 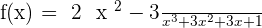
Exercise 3
Determine the domain of the following radical functions:
1 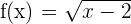
2 
3 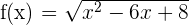
4 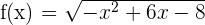
5 
6 
7 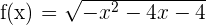
8 
9 
10 
11 
Exercise 4
Determine the domain of the following exponential functions:
1 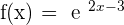
2 
Exercise 5
Determine the domain of the following logarithmic functions:
1 
2 
Exercise 6
Determine the domain of the following trigonometric functions:
1 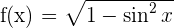
2 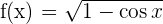
Exercise 7
Determine the domain of the following functions:
1 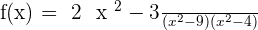
2 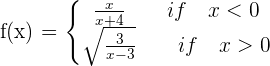
Solution of exercise 1
Determine the domain of the following polynomial functions:
1 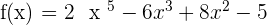

2 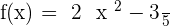

Solution of exercise 2
Determine the domain of the following rational functions:
1 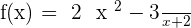
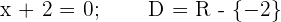
2 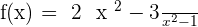
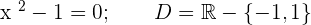
3 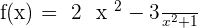
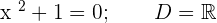
4 
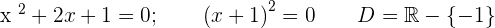
5 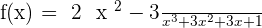
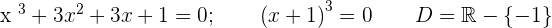
Solution of exercise 3
Determine the domain of the following radical functions:
1 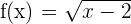

2 

3 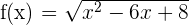
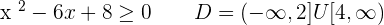
4 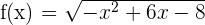

5 

6 

7 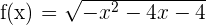
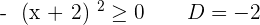
8 

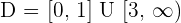
9 

10 
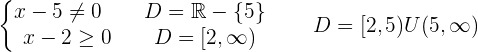
11 
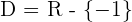
Solution of exercise 4
Determine the domain of the following exponential functions:
1 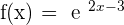

2 

Solution of exercise 5
Determine the domain of the following logarithmic functions:
1 

2 
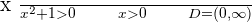
Solution of exercise 6
Determine the domain of the following trigonometric functions:
1 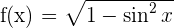
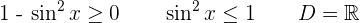
2 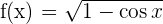
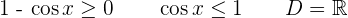
Solution of exercise 7
Determine the domain of the following functions:
1 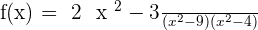

2 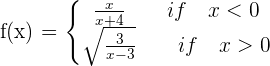

Summarise with AI:













I have math qstn problm
Break even point