Sequences are not limited to finding terms, common divisor or multiple, or finding the first term. There are lots of things that you can find from a sequence. Let's say you have a series that consists of multiples of 2. So, how long will the series go? A time will come when the series will approach infinity, right? But this isn't the case with all series. Some series stops at some point, which means they give the same answer. That is why it becomes important to understand whether the series has a specific limit or not.
The limit of a sequence is a value when a specific sequence either approaches infinity or becomes stable. Since there are two conditions, they have different names. If the sequence goes to infinity, we call it divergent series, on the other hand, if the series converges to a specific value and that value keeps repeating that means it is a convergent series. You can learn more about convergent and divergent series by clicking here.
For example, we have a series here.
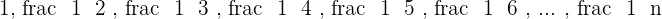
We have our first term which is  , hence:
, hence: 
Our second term is = 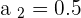
Since we are taking about limit of a sequence, let's pick a big number, how about 1000 = 
That isn't enough to learn about the limit of this sequence, we will pick a very large number this time, how about 1000 000 = 
The limit is 0.
There is another method to find the limit of the sequence but for that you should know about limits.
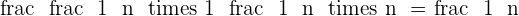

Did you notice something? The limit approached zero that means after some time, the limit will converge to zero hence all the answers that you will get will be zero. Let's take another example:

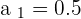
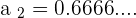
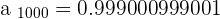
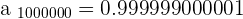
The limit is 1.
From another method:
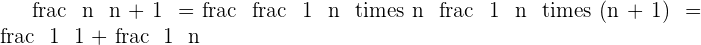
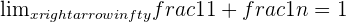
The limit of this series will converge to 1 after some time. Since we talked about converging sequences in both examples, how about considering a divergent sequence?

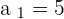

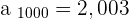
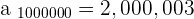
From another method:
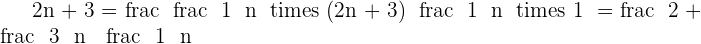

No particular number can represent the limit of this sequence, therefore, the limit is  .
.

Finite Limit of a Sequence
A sequence, 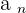 , has a limit, L, if and only if for any positive number,
, has a limit, L, if and only if for any positive number,  , there is a term,
, there is a term, 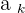 , from which all terms of
, from which all terms of 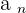 greater than
greater than 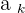 fulfill that
fulfill that  .
.
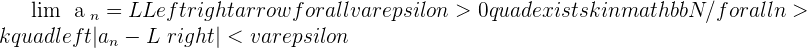
The limit of the sequence 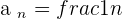 is 0.
is 0.
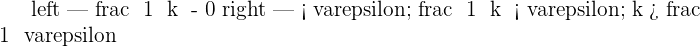
It can be determined from that term of the sequence that the distance from 0 is less than a positive number ( ).
).
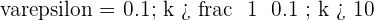
From  , the distance to
, the distance to  is less than
is less than  .
.
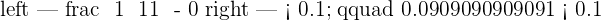
Determine from that term if the distance to  is less than
is less than 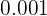 .
.
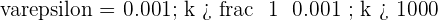
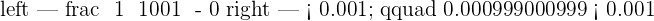
From 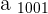 , the distance to
, the distance to  is less than
is less than 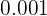 .
.
Infinite Limit of a Sequence
A sequence, 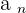 , has a limit of
, has a limit of  when for
when for 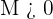 there is a term,
there is a term, 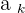 , from which all the terms of
, from which all the terms of 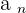 greater than
greater than 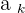 fulfill that
fulfill that 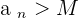 .
.

The limit of the sequence  is
is 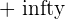 .
.
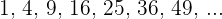
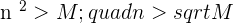
If 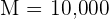 , its square root is
, its square root is  , therefore, for
, therefore, for  it will exceed
it will exceed 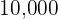 .
.

A sequence, { a }_{ n }, has a limit of 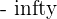 when for
when for  there is a term,
there is a term, 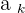 , from which all the terms of
, from which all the terms of 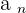 greater than
greater than 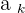 fulfill that
fulfill that  .
.
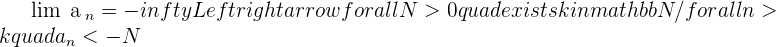
Verify that the limit of the sequence 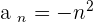 is
is 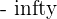 .
.

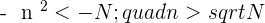
If 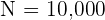 , its square root is
, its square root is  , therefore, for
, therefore, for  it will exceed
it will exceed 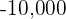 .
.
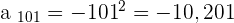













I have math qstn problm
Break even point