Chapters
You are familiar with the derivative of a function. It represents the instantaneous rate of change of a function over a given period. The process of computing the derivatives of the function is known as differentiation. When a function is differentiated once, the resultant derivative is known as the first derivative.
We can further differentiate the first derivative to calculate the second derivative of the function and repeat the process until the function is no longer differentiable. All the derivatives after the first derivative are known as higher-order derivatives. Although the first derivative gives critical information about the function, it does not describe it completely.
In this article, we will discuss the concavity and convexity of the function that are only described by its second derivative.

What are Convex and Concave Functions?
The second derivative of the function depicts how the function is curved, unlike the first derivative, which tells us about the slope of the tangent function. A function that has an increasing first derivative bends upwards and is known as a convex function.
On the other hand, a function that has a decreasing first derivative is known as a concave function and bends downwards. We also describe a concave function as the negative of a convex function. Instead of saying that a function is concave, we can also say that it is concave downwards because a concave function always bends downwards.
In the next section, we will see how to identify the curve of the function and describe it either as a concave or a convex function through its second derivatives.
Theorem
If the function f and its derivative f' can be differentiated at a, then:
- The f is convex at a if
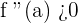
- The f is concave at a if

Now, let us proceed to solve some examples to determine whether the function either as a concave or a convex one.
Example Problems
Identify the curve of the following function and determine whether it is a concave or a convex function:

First, we will compute the first derivative of the function by employing sum/difference and power rules of differentiation:
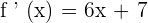
Now, we will differentiate the first derivative further to calculate the second derivative of the function:

Now, compare the results with the above theorem, which says that if the second derivative of a function is greater than zero, then the function is convex. A convex function always bends upwards, so we can conclude that the function  is convex and bends upwards.
is convex and bends upwards.
Identify the curve of the following function and determine whether it is a concave or a convex function:
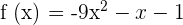
First, we will compute the first derivative of the function by employing sum/difference and power rules of differentiation:
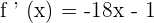
Now, we will differentiate the first derivative further to calculate the second derivative of the function:

Now, compare the results with the above theorem which says that if the second derivative of a function is smaller than zero, then the function is concave. A concave function always bends upwards, so we can conclude that the function 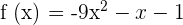 is concave and bends downwards.
is concave and bends downwards.
Intervals of Concavity and Convexity
We use the second derivative and roots of the function to compute the intervals' concavity and convexity of the function. These intervals are also known as points of inflexion. In the next examples, we will see how to determine the intervals of convexity and concavity of the function.
Examples
Study the intervals of concavity and convexity of the following function:

To study the concavity and convexity, perform the following steps:
Step 1 - Find the Second Derivative of a function
To compute the second derivative, we need the first derivative:

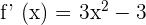
Now, we will differentiate the above derivative further to find the second derivative of the function:
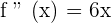
Step 2 - Find the Roots of the Second Derivative
In this step, we will compute the roots or zeroes from the second derivative:

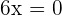

Step 3 - Calculate intervals from the roots
We have got only one root of the function, therefore the intervals will be  and
and 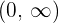 .
.
Step 4 - Substitute the point from each interval in the second derivative
In this step, we will take a point from each interval and substitute it in the second derivative of the function for calculating the concavity and convexity.
Let us take a point -1 from the interval  and substitute it in the second derivative of the function:
and substitute it in the second derivative of the function:
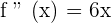

Now, let us take a point 1 from the interval 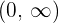 and substitute it in the second derivative of the function:
and substitute it in the second derivative of the function:
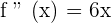

Step 5 - Determine the intervals of convexity and concavity
According to the theorem, if f '' (x) >0, then the function is convex and when it is less than 0, then the function is concave. After substitution of points from both the intervals, the second derivative was greater than 0 in the interval 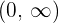 and smaller than 0 in the interval
and smaller than 0 in the interval  . Hence, the intervals of concavity and convexity are:
. Hence, the intervals of concavity and convexity are:
Concavity: 
Convexity: 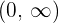
Study the intervals of concavity and convexity of the following function:
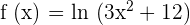
To study the concavity and convexity, perform the following steps:
Step 1 - Find the Second Derivative of a function
To compute the second derivative, we need the first derivative using the chain rule:
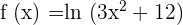
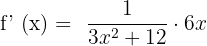
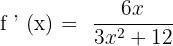
Now, we will differentiate the above derivative further to find the second derivative of the function using the quotient rule:

Step 2 - Find the Roots of the Second Derivative
In this step, we will compute the roots or zeroes from the second derivative. Since the denominator cannot be zero, so we can find roots by setting the numerator equal to 0.
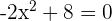
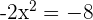
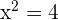
 ,
, 
Hence, we have got two roots of the function 2 and -2.
Step 3 - Calculate intervals from the roots
We have got two roots of the function, therefore we have three intervals  ,
,  and
and 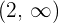 .
.
Step 4 - Substitute the point from each interval in the second derivative
In this step, we will take a point from each interval and substitute it in the second derivative of the function to determine its concavity and convexity.
Let us take a point -3 from the interval  and substitute it in the second derivative of the function:
and substitute it in the second derivative of the function:
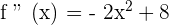
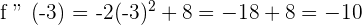
Now, let us take a point 1 from the interval  and substitute it in the second derivative of the function:
and substitute it in the second derivative of the function:


Substitute 3 from the third interval 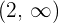 in the second derivative:
in the second derivative:

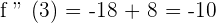
Step 5 - Determine the intervals of convexity and concavity
According to the theorem, if f '' (x) >0, then the function is convex and when it is less than 0, then the function is concave. After substitution, we can conclude that the function is concave at the intervals  and
and 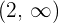 because f '' (x) is negative. Similarly, at the interval (-2, 2) the value of f '' (x) >0, so the function is convex at this interval. Since after substituting 2 and -2 in the second derivative, we get the result 0, hence we will write the intervals of convexity like this:
because f '' (x) is negative. Similarly, at the interval (-2, 2) the value of f '' (x) >0, so the function is convex at this interval. Since after substituting 2 and -2 in the second derivative, we get the result 0, hence we will write the intervals of convexity like this:
Concavity: 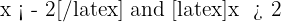
Convexity: 













I have math qstn problm
Break even point