Chapters

What is a Plane?
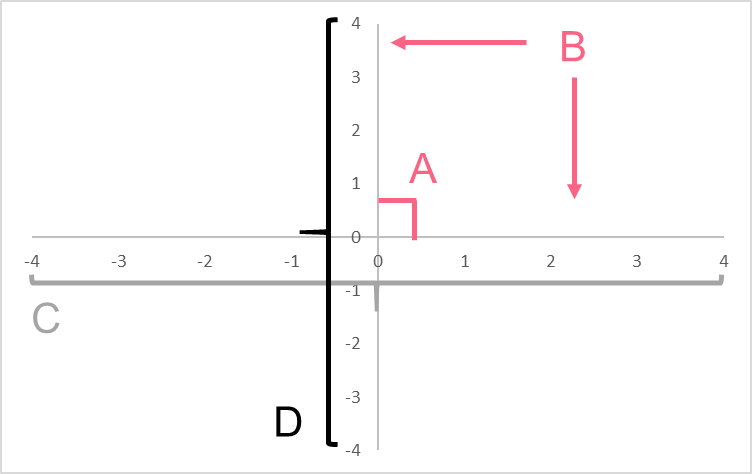
| Property | Example | ||
| A | Two perpendicular lines | Two lines at 90 degrees from each other | X-axis and y axis |
| B | Axes | Axes that have numbers on them | Think of two number lines intersecting each other |
| C | X-axis | Holds x coordinates | For point (3,4), the x coordinate is 3 |
| D | Y-axis | Holds y coordinates | For point (3,4), the y coordinate is 4 |
The Cartesian plane is named after Rene Descartes, a French mathematician. The Cartesian plane is simply referred to as an axis, graph or plot.
Coordinates
The reason we have a graph is to be able to visualize coordinates. You may have heard the word coordinates to describe the physical location of something on earth. For example, global positioning systems, or GPS, use coordinates to locate various things.
Coordinates in math follow the same idea. Let’s start with a simple example: coordinates on a real number line. This is also referred to as a one dimensional coordinate system.
As you can see, a number line can, a number line can include any range of real numbers. A coordinate on a number line is simply one number. Let’s plot three numbers on a number line:
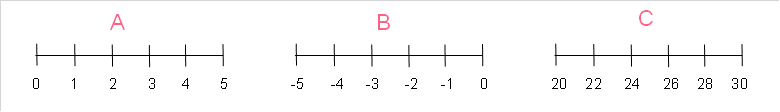

| A | 1 |
| B | 5 |
| C | -3 |
When we talk about coordinates on a Cartesian plane, we are referring to a two-dimensional coordinate system. This means we have two points to graph: an x and a y coordinate.
The x coordinate is always on the left while the y coordinate is always on the right. Let’s take a few examples and graph them:
| A | (4,5) |
| B | (-3,2) |
| C | (0,0) |

Quadrants
Another important property of a graph is that it has 4 quadrants. Take a look below for a definition of what these quadrants mean:

| x | y | |
| Quadrant 1 | 4 | 5 |
| Quadrant 2 | -3 | 2 |
| Quadrant 3 | -4 | -3 |
| Quadrant 4 | 2 | -4 |
The table above gives us the value for each point in the quadrant in the graph. Do you notice any pattern here? Depending on the quadrant, the x and y coordinates will always be either positive or negative. Take a look at the table below.
| x | y | (x,y) | Example | |
| Quadrant 1 | + | + | (+,+) | (4,5) |
| Quadrant 2 | - | + | (-,+) | (-3,2) |
| Quadrant 3 | - | - | (-,-) | (-4,-3) |
| Quadrant 4 | + | - | (+,-) | (2,-4) |
Origin
The origin of a graph is located at the very centre of the plane. Let’s take a look at the origin on the graph.
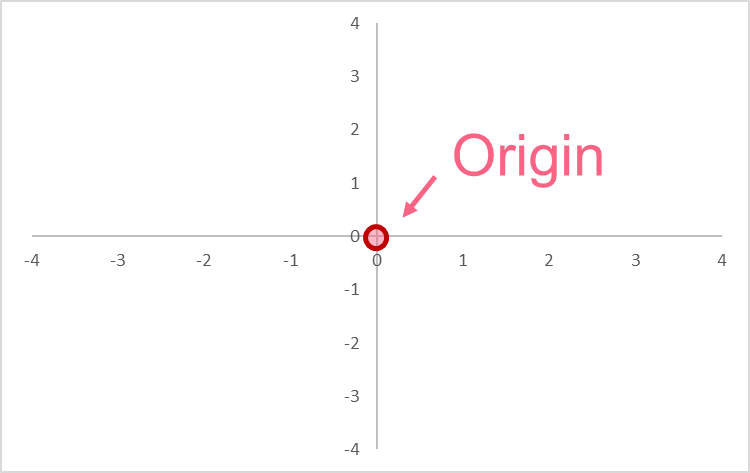
As you can see, the coordinates for the origin are always the same.

The origin is very useful when we want to plot coordinates. It tells us where to start in order to begin moving up or down on the graph. Take a look at the image below for an example.

Horizontal Axis
The x axis is also called the horizontal axis. This is because it lies horizontally on the Cartesian plane. The horizontal axis touches all four quadrants, however it only goes in two directions. Let’s take a look at two examples.
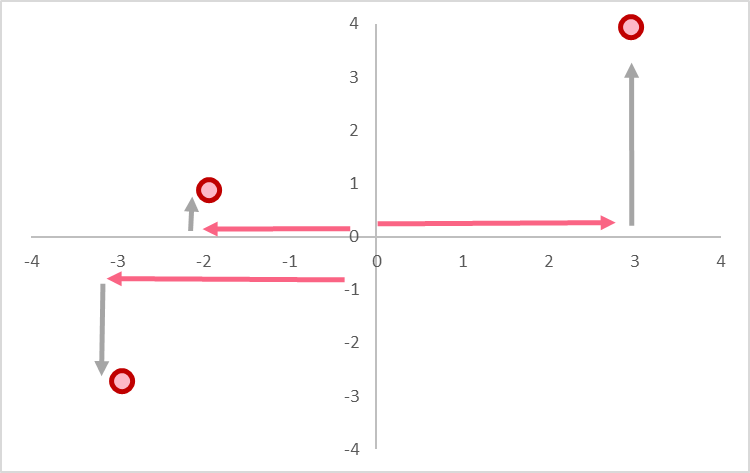
| A | (3,4) | Right 3 |
| B | (-2,1) | Left 2 |
| C | (-3,-3) | Left 3 |
The x coordinate tells us how many places to the left or to the right we have to go.
Vertical Axis
The y axis is also called the vertical axis. This is because it lies vertically on the Cartesian plane. The vertical axis touches all four quadrants, however it only goes in two directions. Let’s take a look at two examples.

| A | (3,4) | Up 4 |
| B | (-2,1) | Up 1 |
| C | (-5,-4) | Down 4 |
The y coordinate tells us how many places up or down we have to go.
Constant
While there are many different types of functions we can graph on a plane, the most common one is a linear function. A linear function involves any straight line relationship, whose standard form is written as follows:

If we were to plug in values for the x variable, we get a corresponding y variable. A line is essentially a set of coordinates that can be connected together.
| x | y | |
| A | 1 | 7 |
| B | 2 | 10 |
| C | 3 | 13 |
| D | 4 | 16 |
| E | 5 | 19 |
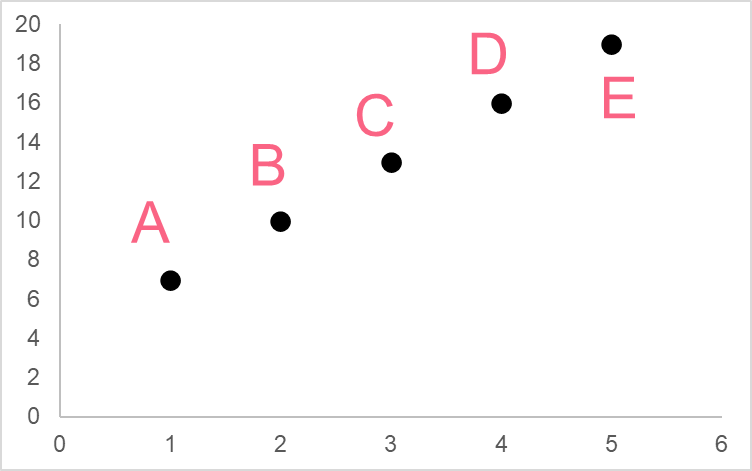
Sometimes, however, we have a linear equation that only has two elements: the y variable and a constant term.
This graph looks like just a straight line. Let’s take a look at a few examples.
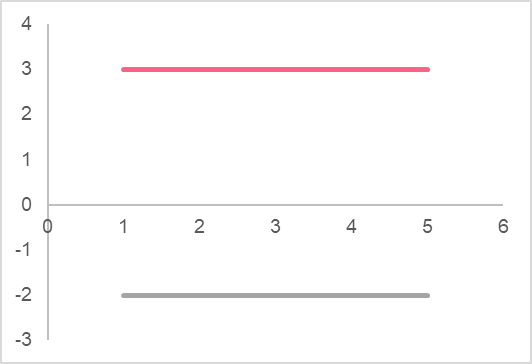
| A | B |
| y = 3 | y = -2 |
Example 1
Let’s test our knowledge on quadrants. Looking at the quadrant specified below, can you give a list of coordinates that would belong to this quadrant?
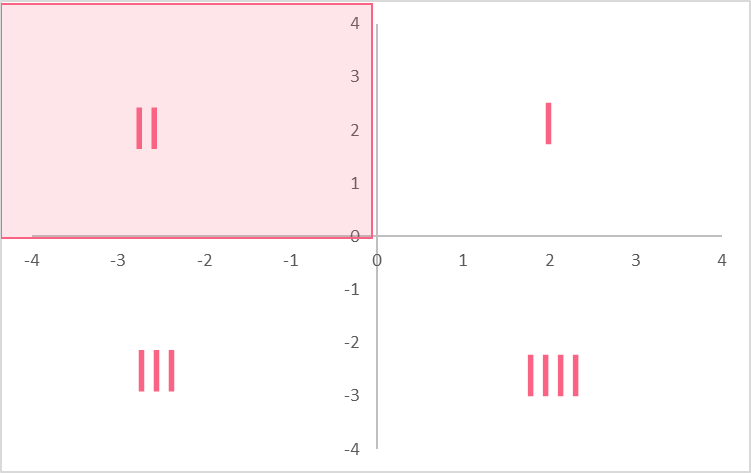
Here are some possible answers:
- (-5,3)
- (-2, 10)
- (-7,8)
Example 2
- (-5, -5)
- (-2, -1)
- (-6, -3)
Because both the x and y values have a negative value, we are looking at the 3rd quadrant.
Example 3
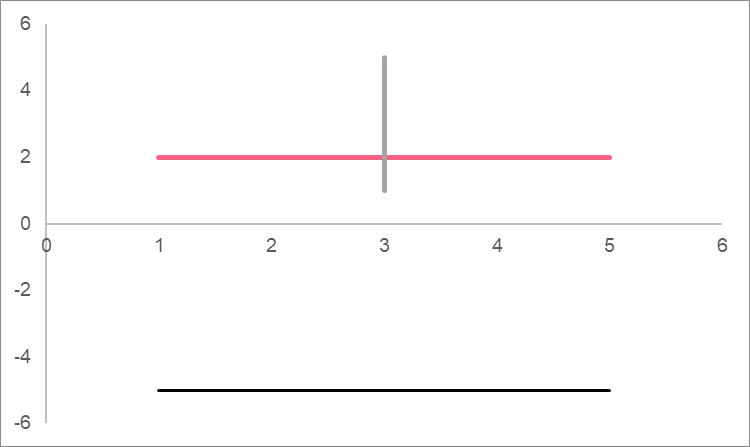
Constants can sometimes be tricky. Graph the following constants:
| A | B | C |
| y = 2 | x = 3 | y = -5 |
Because x and y are constants here, we draw horizontal and vertical lines.
Example 4
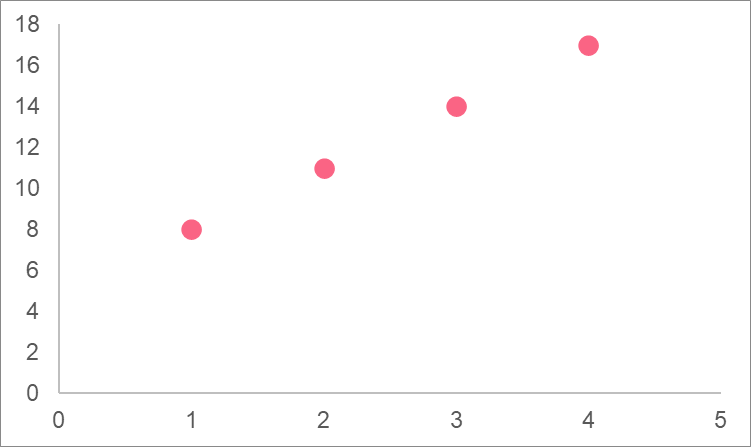
Let’s plot the coordinates to the following equation.
\[
y = 3x + 5
\]
Here is the graph:













I have math qstn problm
Break even point