If you came here, you know what are limits and their fundamentals. If you don't know about limits, it is better to learn limits in detail in order to understand this rule. Let's say we have two equations that have a limit condition, 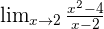 . If we plugged the value of x in the equation, it will result in
. If we plugged the value of x in the equation, it will result in 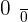 and we all know that
and we all know that 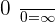 . We can't just leave the answer to infinity, we need a value before the function reaches infinity. Let's pick another example, we have a function with a limit,
. We can't just leave the answer to infinity, we need a value before the function reaches infinity. Let's pick another example, we have a function with a limit, 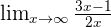 . Plugging the value of x will only result in
. Plugging the value of x will only result in  which can give us any number, the answer will have a lot of possibilities. These answers are not acceptable especially in the case of applied physics, that is where we use L'Hôpital's rule to narrow down our answer.
which can give us any number, the answer will have a lot of possibilities. These answers are not acceptable especially in the case of applied physics, that is where we use L'Hôpital's rule to narrow down our answer.
L'Hôpital's rule gives you the answer before the function reaches infinity. That value is way more valuable than the answer we get (which is ambiguous, hence we can't learn anything from it). Suppose you have two functions,  and
and  and when applying limits, you get answers in these forms,
and when applying limits, you get answers in these forms, 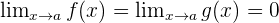 or it can be
or it can be  , we will use L'Hôpital's rule.
, we will use L'Hôpital's rule.
We will use the help of calculus and differentiate both functions and if 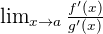 exists, this limit coincides with
exists, this limit coincides with 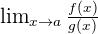 .
.
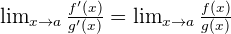
To apply the L'Hôpital's rule, there must be a limit in the form 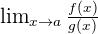 , where a can be a number or infinite and have the indeterminate forms:
, where a can be a number or infinite and have the indeterminate forms:

One of the biggest frequently asked questions is that if you take derivatives on both functions yet your answer is infinity then what to do? Keep taking derivatives on both functions until you achieve a unique answer. The degree of derivative doesn't matter here, what matters is either you approach a unique answer or not. Eventually, you will reach zero if the function keeps giving you infinity.

Examples
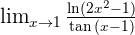
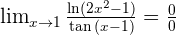

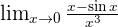


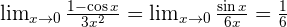


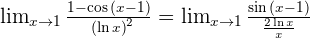

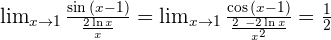
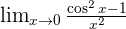
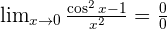


Infinity Minus Infinity
For the indeterminate form of infinity minus infinity, the fractions put themselves into a common denominator.


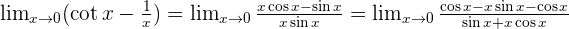

Zero Times Infinity
The indeterminate form of zero times infinity is transformed as follows:
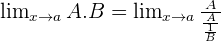
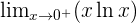
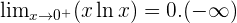



Indeterminate Forms 0º, ∞º, and 1^∞
In the indeterminate forms zero to the power of zero, infinity to the power of zero and one to the power of infinity; make the following transformations:

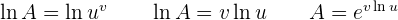
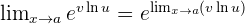
___________________________________________________________________________________________________________________________
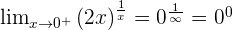
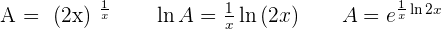
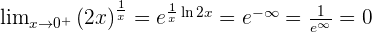
____________________________________________________________________________________________________________________________
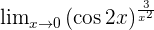
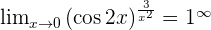

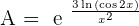
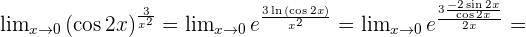

_____________________________________________________________________________________________________________________________
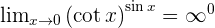

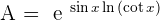
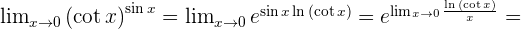
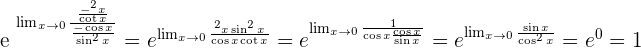
Summarise with AI:












I have math qstn problm
Break even point