A function has a range and domain. The domain will tell you the range of the function. In simple words, the number of input will show you the range of the function. Sometimes, mathematicians are not interested in the whole range, they are interested in the highest and lowest range of the function. We call both ranges bounded. The word bound explains that the function will be bounded from the highest specific range to the lowest specific range. It means that the answers of that function will lie between both values. To calculate the bounds of a function, you need to find the highest bound as well as the lowest bound.

Bounded from Above
Let's say we have a function. The function is defined on  . It means that the function contains all the real values till infinity. A function is bounded above if there is a real number, k, such that for all of x,
. It means that the function contains all the real values till infinity. A function is bounded above if there is a real number, k, such that for all of x, 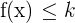 . The number k is called the upper bound.
. The number k is called the upper bound.
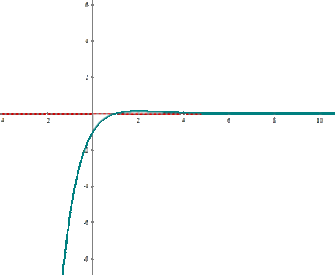
In the above example, the peak point is  . Hence, we can say
. Hence, we can say 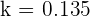 .
.
Bounded from Below
Imagine another function and that function is also defined on  . A function is bounded below if there is a real number, k', such that for all of x,
. A function is bounded below if there is a real number, k', such that for all of x,  . The number k' is called the lower bound.
. The number k' is called the lower bound.
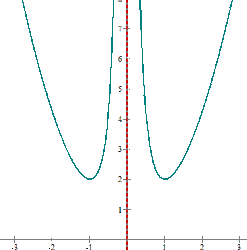
In the above example, the lowest point is  . Hence, we can say
. Hence, we can say 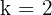 .
.
Bounded Function
The proper way to define a bounded function is to range it from lower bound to higher bound. This is how to bound a function:


The highest value of the function in the above example is  , however, the lowest value is
, however, the lowest value is 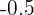 . The right way to write a bounded function is like this:
. The right way to write a bounded function is like this:














I have math qstn problm
Break even point