Chapters
Data interpretation is very important whether you are an industrialist or a social worker. There will be a time when you will be given a lot of data. Let's say you are working as an animal expert who is trying to preserve a species from extinction. You have a pair in your shelter. You predicted that a pair of that species can produce 4 offsprings maximum. Those 4 offsprings will have 16 offsprings in future. This goes on but there is an arrangement in these numbers. It would be something like this:
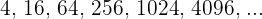
Neglecting the possibility of infant death, you predicted the future. You know that the future of this species is secured now. What you did is that you used the sequence to predict the future of that species. A sequence is a set of numbers arranged one after another. Every number in the term is related to its previous number. For example, 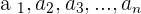 . The numbers
. The numbers  are the terms of the sequence and the subscript is the set of positive integers. Those integers indicate the place that a term occupies in the sequence.
are the terms of the sequence and the subscript is the set of positive integers. Those integers indicate the place that a term occupies in the sequence. 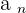 means the
means the 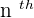 term in the sequence. There are different types of sequences but in this lecture, we will focus on the most common sequences that are used and they are:
term in the sequence. There are different types of sequences but in this lecture, we will focus on the most common sequences that are used and they are:
- Arithmetic Sequence.
- Geometric Sequence.
- Harmonic Sequence.
- Fibonacci Sequence.

Using Formulas
Suppose you are interested in a specific term, not the whole sequence, you can find that term without making the whole sequence by using formulas. Furthermore, you can also find the sum of the whole sequence with just a formula. In addition, you can find whether the sequence is reaching its limit or it will go up to infinity. This information is very important, however, there are some points to be noted. First of all, every sequence is unique which means every sequence has different formulas for different purposes. You can't use the term formula of arithmetic sequence for harmonic sequence and vice versa. Identification of a series is very important and also a common mistake. Hence, the first step is to recognize the series first then check which formula is suitable.
Calculation of a Sequence: By the Nth Term
Let's say you are asked to make a series and all you are given is a formula. With the help of that, you can make a series .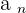 is a criterion that allows us to calculate any term of the sequence.
is a criterion that allows us to calculate any term of the sequence.
Example

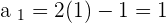
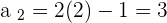
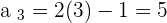
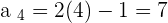
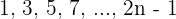
Not all sequences have a general term. For example, the sequence of prime numbers:
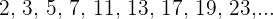
Recursive Formula
Sometimes, things don't increase or decrease because of a common ratio, they alter because of their previous term. For example, buttercups petals grow according to the preceding term and buttercup is not the only flower that follows this sequence, many other flowers follow this sequence too such as lilies, iris, daisies, and many more. A recursive formula can be divided into two parts, the starting term and an equation defining  in terms of previous terms. For example:
in terms of previous terms. For example:
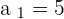

We have the recursive formula now, we can find the rest of the series.
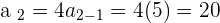
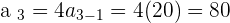
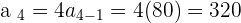
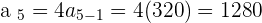
Did you notice that each term is found by preceding term. Only the first term is required and you can find the whole series from the preceding term.
Example
Write a sequence whose first term is 2, knowing that each term is the square of the previous term.



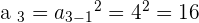
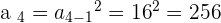


Fibonacci Sequence or Fibonacci Number
Fibonacci sequence is the biggest example of recursive formula. The Fibonacci number follows the sequence by adding the previous two terms. Here is the series:
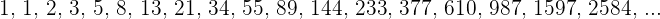
The first two terms were 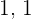 , adding both terms will result in
, adding both terms will result in  . Now the previous two terms are
. Now the previous two terms are  , adding them will result in
, adding them will result in  . This time the previous two terms are
. This time the previous two terms are 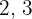 , add them and you will get
, add them and you will get  and this keeps going on forever. In simple words, the first two terms are one and the other terms are obtained by adding the two previous terms.
and this keeps going on forever. In simple words, the first two terms are one and the other terms are obtained by adding the two previous terms.

To add terms, you need to know the terms. For example, your teacher asked you to add 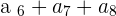 . If you don't know these terms then the first thing is to find these terms. After making the series, we found that
. If you don't know these terms then the first thing is to find these terms. After making the series, we found that 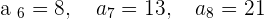 , now add them.
, now add them.
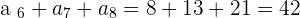












I have math qstn problm
Break even point