Chapters

Exercise 1
Prove that the sequence 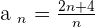 has a limit of
has a limit of  . Also, calculate the terms whose distance from
. Also, calculate the terms whose distance from  is less than
is less than  .
.
Exercise 2
Prove that the sequence 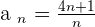 has a limit of
has a limit of  and calculate how many terms of the succession are not within
and calculate how many terms of the succession are not within  .
.
Exercise 3
Prove that the sequence 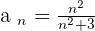 has a limit of
has a limit of  and calculate how many terms of the succession are not within
and calculate how many terms of the succession are not within 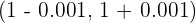 .
.
Exercise 4
Prove that  . Also, calculate the terms whose distance from the limit is less than
. Also, calculate the terms whose distance from the limit is less than 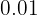 .
.
Exercise 5
Prove that the sequence 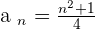 has a limit of
has a limit of  and determine how many terms in the sequence are less than a million?
and determine how many terms in the sequence are less than a million?
Exercise 6
Prove that the sequence 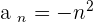 a has a limit of
a has a limit of  . Also, what term of the sequence produces values of less than
. Also, what term of the sequence produces values of less than 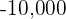 ?
?
Solution of exercise 1
Prove that the sequence 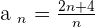 has a limit of
has a limit of  . Also, calculate the terms whose distance from
. Also, calculate the terms whose distance from  is less than
is less than  .
.
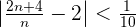

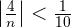
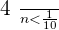
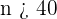
From 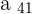 the distance to
the distance to  is less than
is less than 
Solution of exercise 2
Prove that the sequence 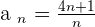 has a limit of
has a limit of  and calculate how many terms of the succession are not within
and calculate how many terms of the succession are not within  .
.
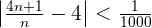

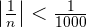
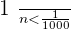

The first thousand terms of the sequence are out.
Solution of exercise 3
Prove that the sequence 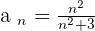 has a limit of
has a limit of  and calculate how many terms of the succession are not within
and calculate how many terms of the succession are not within 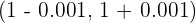 .
.


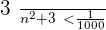
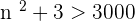


The first  terms are out.
terms are out.
Solution of exercise 4
Prove that  . Also, calculate the terms whose distance from the limit is less than
. Also, calculate the terms whose distance from the limit is less than 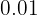 .
.
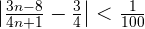
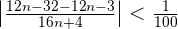
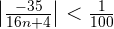
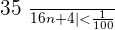
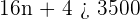
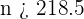
From 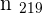 the distance to the limit is less than
the distance to the limit is less than 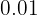 .
.
Solution of exercise 5
Prove that the sequence 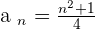 has a limit of
has a limit of 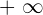 and determine how many terms in the sequence are less than a million?
and determine how many terms in the sequence are less than a million?
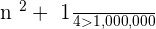

The 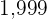 first terms of the sequence.
first terms of the sequence.
Solution of exercise 6
Prove that the sequence 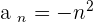 a has a limit of
a has a limit of  . Also, what term of the sequence produces values of less than
. Also, what term of the sequence produces values of less than 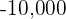 ?
?

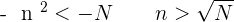
If 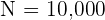 , its square root is
, its square root is  , therefore,
, therefore,  a101 will be less than
a101 will be less than 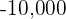 .
.
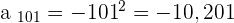













I have math qstn problm
Break even point