A function is a relation between input and output. It means that whether input you will give it, it will give you a result. What if, we have the output but we want to find the result? The real question is, it is possible to get input by putting the output? The answer is yes. There is a method through which we can get the input and that method is called inversing a function. Basically, an inverse function is a function that can reverse the normal function. For example, look at the bottom picture.
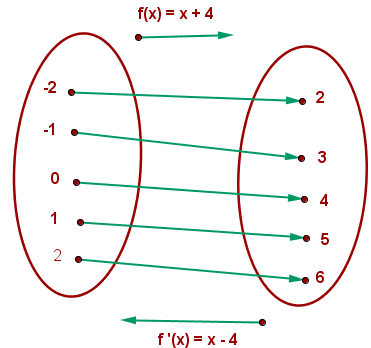
We have a function that is  . We have its inputs and outputs. If we input the value
. We have its inputs and outputs. If we input the value  , we will get
, we will get  which is the output. However, we have the
which is the output. However, we have the  as output but we want to find the input of the output (which is
as output but we want to find the input of the output (which is  ). To find that input, we will reverse the function. There is a method of reversing a function which we will discuss in this resource. After reversing, you got the anti-function (another name for inverse function) which is
). To find that input, we will reverse the function. There is a method of reversing a function which we will discuss in this resource. After reversing, you got the anti-function (another name for inverse function) which is  . Now let's put the output in this function.
. Now let's put the output in this function.
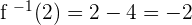
We got our input back! You can check this function by placing all other outputs and you will receive input in the end. In short, if 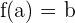 that means that
that means that 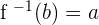 . An inverse function is represented by a
. An inverse function is represented by a  as the function's power, like this
as the function's power, like this 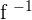 .
.
Note that:
- The domain
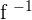 is the range of f.
is the range of f. - The range of
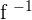 is the domain of f.
is the domain of f. - To find the range of a function we have to find the domain of its inverse function.
- If two functions are the inverse of each other, their composition is the identity function. (i.e.
 )
) - The graphs of
 and
and 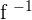 are symmetrical about the bisector of the first and third quadrant.
are symmetrical about the bisector of the first and third quadrant.

We must distinguish between the inverse function, f−1(x), and the inverse of a function, 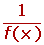

How To Calculate Inverse of a Function
To make it easier for you, we broke the whole method into steps to calculate the anti-function of a function.
Step 1: Replace the function with y
For example, you have a function, 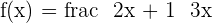 . Replace the function with y:
. Replace the function with y:
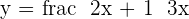
Step 2: Make the equation interms of x
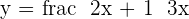

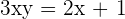

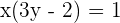
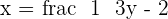
Step 3: Replace the x with f−1(x) and y with x
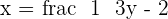
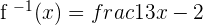
And that is how to find an inverse of a function!
Step 4(Optional): Verification
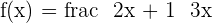
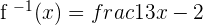
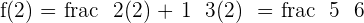
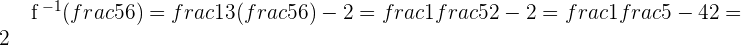
Hence it is verified!
Examples



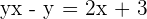

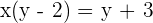

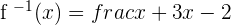
Check the result for x = 2.
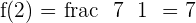
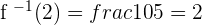

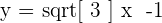

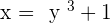
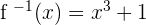
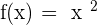
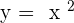
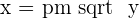














I have math qstn problm
Break even point