
Introduction
In the real world, things often change at a steady rate. Whether it is a taxi fare that charges a base fee plus a rate per mile, or a plant growing a fixed amount every week, these scenarios can be described using mathematics.
These relationships are known as linear functions. Humans are naturally good at spotting these patterns, but in algebra, we write them down as equations so we can make precise predictions.
In these problems, we are usually looking for two specific things: a starting value (often called the y-intercept) and a rate of change (often called the slope or gradient).
Understanding the Equation
Most linear word problems can be solved using the slope-intercept form of a straight line:

(Note: In some textbooks, this is written as y = mx + b).
Here is what each letter represents in a real-world context:
- y (The Dependent Variable): The final result or total amount (e.g., Total Cost, Total Height).
- x (The Independent Variable): The variable that changes (e.g., Time, Distance, Number of items).
- m (The Slope/Rate): How much y changes for every 1 unit of x (e.g., Cost per mile, Growth per week).
- c (The Y-Intercept): The starting value when x = 0 (e.g., The base fee, the initial height).
Worked Example
A local gym charges a joining fee of £50 and then a monthly membership cost of £30.
- Write an equation for the total cost, C, after n months.
- Calculate the total cost for a member who stays for 2 years.
Solution:
Part 1: The Equation
First, identify the components of the linear function.
The joining fee is a one-off payment. This is our starting value (c):
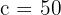
The monthly cost is the rate of change. It increases the total cost by £30 every month (m):
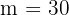
The variables are n (months) and C (Total Cost).
Substitute these into the standard formula:
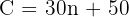
Part 2: Calculating Cost
We need to find the cost for 2 years. First, convert years to months because our rate is monthly.
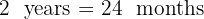
So:
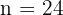
Substitute this into the equation:
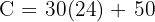
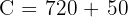
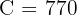
Answer:
The equation is C = 30n + 50 and the total cost for 2 years is £770.
Practice Problems & Solutions
Three kilograms (kg) of squid can be purchased at the market for £18. Determine the equation and represent the function that defines the cost (y) based on weight (x).
This is a problem of direct proportion. There is no "base fee" mentioned, so if you buy 0 squid, the cost is 0. This means the y-intercept (c) is 0:
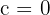
We need to find the rate (m), which is the cost per kg:
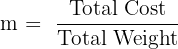
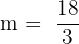
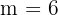
So, the cost is £6 per kg. Substitute m = 6 and c = 0 into the linear equation:
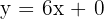
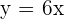
It has been observed that a particular plant's growth is linear. It measured 12 cm when it arrived at the nursery and 15.5 cm exactly one week later.
Determine the function h(t) that represents the plant's growth over time t (in weeks).
The initial height (when t = 0) is the y-intercept:
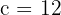
To find the rate of growth (m), we look at the change over one week:
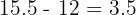
The plant grows 3.5 cm per week:
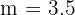
The equation is:
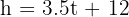
A car rental charge is £40 per day plus £0.50 per kilometre (km) travelled.
Determine the equation of the line that represents the daily cost (C) by the number of kilometres travelled (x).
If a total of 300 km was travelled in one day, how much is the rental company going to receive as a payment?
1.The fixed daily charge is the y-intercept:
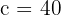
The cost per km is the slope:
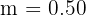
The equation is:
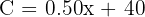
2. Substitute x = 300 into the equation:
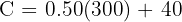
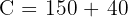
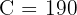
Answer: The rental company receives £190.
When digging into the earth, assume the temperature rises according to the following linear equation:
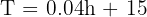
Where T is the temperature in degrees celsius and h is the depth in metres.
Calculate:
What the temperature will be at a depth of 600 m?
At what depth would there be a temperature of 100 degrees celsius?
Substitute h = 600 into the equation:
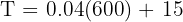
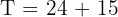
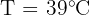
For depth at 100 degrees, substitute T = 100:
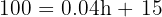
Subtract 15 from both sides:
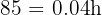
Divide by 0.04:
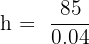
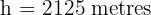
The pollution level in the centre of a city at 06:00 is 30 ppm (parts per million) and it grows in a linear fashion by 5 ppm every hour.
Let y be pollution and t be the time elapsed (in hours) after 06:00.
Determine the equation that relates y with t.
Calculate the pollution level at 16:00 (4 o'clock in the afternoon).
The starting level at t = 0 (06:00) is:
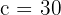
The rate of growth per hour is:

The equation is:
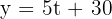
2. To find pollution at 16:00, calculate how many hours have passed between 06:00 and 16:00:
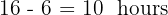
So:
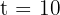
Substitute this into the equation:
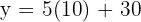
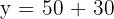
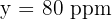












I have math qstn problm
Break even point