Chapters
- Calculate the X- and Y-Intercepts of the Following Functions:
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10
- Solution of exercise 11

The best Maths tutors available
Calculate the X- and Y-Intercepts of the Following Functions:
Exercise 1
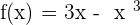
Exercise 2
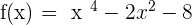
Exercise 3
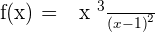
Exercise 4

Exercise 5
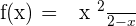
Exercise 6
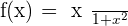
Exercise 7
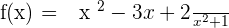
Exercise 8

Exercise 9
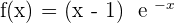
Exercise 10
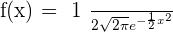
Exercise 11
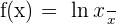
Solution of exercise 1
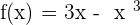
x-intercepts:

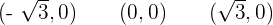
y-intercept:

Solution of exercise 2
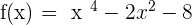
x-intercepts:
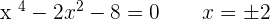

y-intercept:

Solution of exercise 3
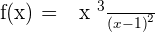
x-intercepts:
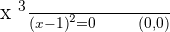
y-intercept:

Solution of exercise 4

x-intercepts:

No x-intercepts.
y-intercept:
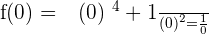
No y-intercept.
Solution of exercise 5
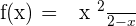
x-intercepts:

y-intercept:

Solution of exercise 6
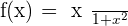
x-intercept:
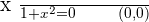
y-intercept:
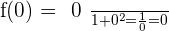

Solution of exercise 7
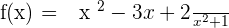
x-intercepts:


y-intercept:
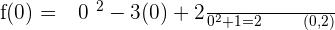
Solution of exercise 8

x-intercepts:
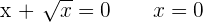

y-intercept:

Solution of exercise 9
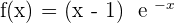
x-intercepts:
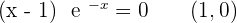
y-intercept:
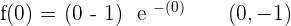
Solution of exercise 10
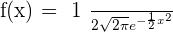
x-intercepts:

When we will take 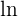 on both sides, the right-hand-side will be equal to infinity hence no x-intercept.
on both sides, the right-hand-side will be equal to infinity hence no x-intercept.
y-intercept:
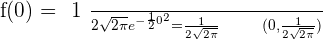
Solution of exercise 11
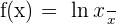
x-intercepts:
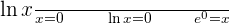

y-intercept:
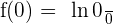
No y-intercept
Summarise with AI:












I have math qstn problm
Break even point